题目内容
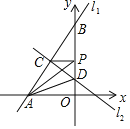
【题目】已知直线![]() :
:![]() 与直线
与直线![]() :
:![]() 都经过
都经过![]() ,直线
,直线![]() 交y轴于点
交y轴于点![]() ,交x轴于点A,直线
,交x轴于点A,直线![]() 交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:①方程组
交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:①方程组 的解为
的解为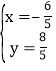 ;②
;②![]() 为直角三角形;③
为直角三角形;③![]() ;④当
;④当![]() 的值最小时,点P的坐标为
的值最小时,点P的坐标为![]() 其中正确的说法个数有
其中正确的说法个数有![]()
![]()
A. 1个B. 2个C. 3个D. 4个
【答案】D
【解析】
根据一次函数图象与二元一次方程的关系,利用交点坐标可得方程组的解;根据两直线的系数的积为![]() ,可知两直线互相平行;求得BD和AO的长,根据三角形面积计算公式,即可得到
,可知两直线互相平行;求得BD和AO的长,根据三角形面积计算公式,即可得到![]() 的面积;根据轴对称的性质以及两点之间,线段最短,即可得到当
的面积;根据轴对称的性质以及两点之间,线段最短,即可得到当![]() 的值最小时,点P的坐标为
的值最小时,点P的坐标为![]() .
.
解:![]() 直线
直线![]() :
:![]() 与直线
与直线![]() :
:![]() 都经过
都经过![]() ,
,
![]() 方程组
方程组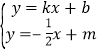 的解为
的解为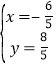 ,
,
故①正确;
把![]() ,
,![]() 代入直线
代入直线![]() :
:![]() ,可得
,可得
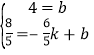 ,解得
,解得![]() ,
,
![]() 直线
直线![]() :
:![]() ,
,
又![]() 直线
直线![]() :
:![]() ,
,
![]() 直线
直线![]() 与直线
与直线![]() 互相垂直,即
互相垂直,即![]() ,
,
![]() 为直角三角形,
为直角三角形,
故②正确;
把![]() 代入直线
代入直线![]() :
:![]() ,可得
,可得![]() ,
,
![]() 中,令
中,令![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
在直线![]() :
:![]() 中,令
中,令![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故③正确;
点A关于y轴对称的点为![]() ,
,
设过点C,![]() 的直线为
的直线为![]() ,则
,则
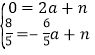 ,解得
,解得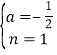 ,
,
![]() ,
,
令![]() ,则
,则![]() ,
,
![]() 当
当![]() 的值最小时,点P的坐标为
的值最小时,点P的坐标为![]() ,
,
故④正确.
故选:D.


练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目