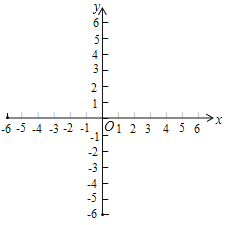题目内容
【题目】在平面直角坐标系
中，对于点
与图形
，若点
为图形上任意一点， 点关于第一、三象限角平分线的对称点为
，且线段
的中点为
，则称点是图形关于点的“关联点”
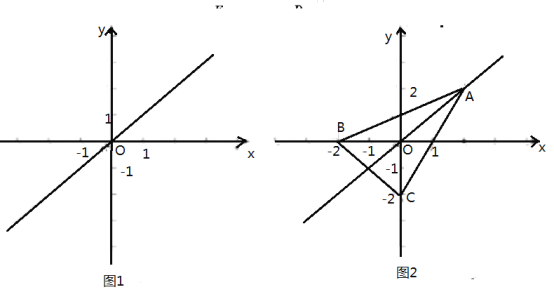
（1）如图1，若点是点
关于原点的关联点，则点的坐标为
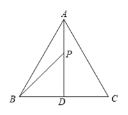
（2）如图2，在
中，
①将线段
向右平移
个单位长度，若平移后的线段上存在两个关于点
的关联点，则
的取值范围是
②已知点
和点
，若线段
上存在关于点
的关联点，求
的取值范围．
【答案】（1）
；（2）①
；②
或
．
【解析】
（1）设点P坐标为（a，b），根据“关联点”的定义、中点的坐标公式和关于第一、三象限角平分线对称的两点的坐标规律即可；
（2）①先求出原AC与x轴的交点，然后根据△ABC是轴对称图形，且对称轴为第一、三象限角平分线和“关联点”的定义可得：“关联点”定义中的
为OA关于（2,0）的对称线段
与△ABC边的交点，平移线段可发现：当
在C的左侧，
过点（1,0）或（1,0）的右侧时符合题意，再列出不等式即可；
②由S、T的坐标可知，线段ST是x轴的一部分，线段ST关于点N的对称线段
也是x轴的一部分，从而判断出定义中是△ABC边与x轴的交点，由图可知：点只有（-2,0）与（1,0）两种可能，再根据线段需要过点（-2,0）或（1,0）分类讨论并列出不等式即可．
解：（1）设点P坐标为（a，b）
∵点
关于第一、三象限角平分线的对称点为，
∴
，
∵点
是点
关于原点的关联点，
∴
的中点为原点，
∴
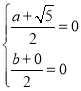，解得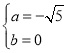
∴点P坐标为：
故答案为：
（2）①设原AC的解析式为y=kx+b，
将
代入得：
，解得：
∴原直线AC的解析式为：y=2x-2，
当y=0时，解得：x=1，
∴原AC与x轴的交点为（1,0）
△ABC是轴对称图形，且对称轴为第一、三象限角平分线和“关联点”的定义可得：定义中的Q在△ABC边上，
∴也在△ABC的边上，
∵将线段AO向右平移d(d>0)个单位长度，若平移后的线段上存在两个△ABC关于点（2,0）的关联点，
∴点和线段OA上的点必关于点（2,0）对称，此时O点坐标为（d,0），A点坐标为（2+d,2），
故作出OA关于（2,0）的对称线段，其中
，
，
也必在上，即点为与△ABC边的交点，
∵平移后的线段上存在两个
关于点
的关联点，
∴与△ABC边必须有两个交点才满足题意，
如图中蓝线所示，平移可发现，当与C重合时，与△ABC边有一个交点，继续向左平移即可有两个交点，当过点（1,0）也有两个交点，继续向左平移就只有一个交点，
故当在C的左侧，过点（1,0）或（1,0）的右侧时符合题意，
，解得：．
故答案为：
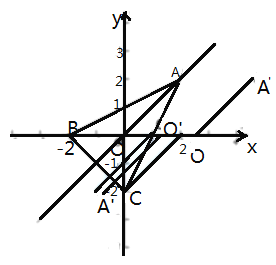
②∵点
和点
∴线段ST是x轴的一部分
∴线段ST上存在△ABC关于点N（n,0）的关联点，
故S、T关于点N（n,0）的对称点
坐标为（n-2,0），
坐标为（n-4,0）定义中在线段上，
∴即为△ABC边与x轴的交点，
由图可知，点只有（-2,0）与（1,0）两种可能，
∴线段需要过点（-2,0）或（1,0），
当线段需要过点（-2,0）时，
，解得
当线段需要过点（1,0）时，
，解得，
综上所述：或．
