题目内容
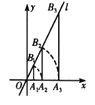
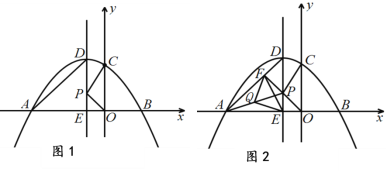
【题目】如图1,抛物线![]() 与x轴交于A、B两点(点A在x轴的负半轴),与y轴交于点C
与x轴交于A、B两点(点A在x轴的负半轴),与y轴交于点C![]() . 抛物线的对称轴交抛物线于点D,交x轴于点E,点P是线段DE上一动点(点P不与DE两端点重合),连接PC、PO.
. 抛物线的对称轴交抛物线于点D,交x轴于点E,点P是线段DE上一动点(点P不与DE两端点重合),连接PC、PO.
(1) 求抛物线的解析式和对称轴;
(2) 求∠DAO的度数和△PCO的面积;
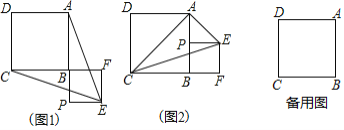
(3) 在图1中,连接PA,点Q 是PA 的中点.过点P作PF⊥AD于点F,连接QE、QF、EF得到图2.试探究: 是否存在点P,使得![]() ,若存在,请求点P的坐标;若不存在,请说明理由.
,若存在,请求点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;
;![]() ;(2)45°;
;(2)45°;![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)把C点坐标代入![]() 解出解析式,再根据对称轴
解出解析式,再根据对称轴![]() 即可解出.
即可解出.
(2)把A、D、E、C点坐标求出后,因为AE=DE,且DE⊥AE,所以∠DAO=![]() ,P点y轴的距离等于OE,即可算出△POC的面积.
,P点y轴的距离等于OE,即可算出△POC的面积.
(3)设出PE=m,根据勾股定理用m表示出PA,根据直角三角形斜边中线是斜边的一半可以证明AQ=FQ=QE=QP,所以△AQF和△AQE都是等腰三角形,又因为∠DAO=![]() ,再根据角的关系可以证明△FEQ是等腰直角三角形,再根据
,再根据角的关系可以证明△FEQ是等腰直角三角形,再根据![]() ,解出m即可.可以通过圆的性质,来判断△FEQ是等腰直角三角形,再根据
,解出m即可.可以通过圆的性质,来判断△FEQ是等腰直角三角形,再根据![]() 建立等式算出m即可.
建立等式算出m即可.
解: (1) 将C![]() 代入
代入![]() 求得a=
求得a=![]() ,
,
∴抛物线的解析式为![]() ;
;
由![]() 可求抛物线的对称轴为直线
可求抛物线的对称轴为直线![]()
(2) 由抛物线可求一些点的坐标: ![]()
∴ AE=DE=3,又DE⊥AE
∴△ADE是等腰直角三角形 ∴∠DAO=45°
作PM⊥y轴于M,在对称轴上的点P的横坐标为-1,∴PM=1,又OP=![]()
∴△OPC的面积为![]()
(3)解:存在点![]() 满足题目条件.
满足题目条件.
解法一: 设点P的纵坐标为m(0<m<3),则PE=m,
∵点Q是PA的中点,∴QE、QF分别是Rt△PAE、Rt△PAF的公共斜边PA上的中线
∴QE=QF=AQ=PQ=![]()
∵QE=AQ,QF=AQ ∴∠EAQ=∠AEQ,∠FAQ=∠AFQ
∴∠EQP=2∠EAQ,∠FQP=2∠FAQ
∴∠EQF=2(∠EAQ + ∠FAQ ) =2∠DAO=90°
又∴QE=QF ∴△EFQ是等腰直角三角形
∴△EFQ的面积为![]()
由![]() 得
得![]() 解得
解得![]()
∵0<m<3 ∴![]() ∴在抛物线对称轴上的点P的坐标为
∴在抛物线对称轴上的点P的坐标为![]()
解法二: 设点P的纵坐标为m(0<m<3),则PE=m,![]()
∵点Q是PA的中点,∴QE、QF分别是Rt△PAE、Rt△PAF的公共斜边PA上的中线
∴QE=QF=AQ=PQ=![]()
∴四边形PEAF内接于半径为QE的⊙Q,
∴∠EQF=2∠DAO=90°
又∴QE=QF ∴△EFQ是等腰直角三角形
∴△EFQ的面积为![]()
由![]() 得
得![]() 解得
解得![]()
∵0<m<3 ∴![]() ∴在抛物线对称轴上的点P的坐标为
∴在抛物线对称轴上的点P的坐标为![]()