题目内容
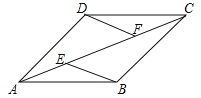
【题目】已知，如图，在四边形ABCD中，AB∥CD，E，F为对角线AC上两点，且AE=CF，DF∥BE，AC平分∠BAD．求证：四边形ABCD为菱形．
【答案】证明见试题解析．
【解析】
试题分析：首先证得△ABE≌△CDF，得到AB=CD，从而得到四边形ABCD是平行四边形，然后证得AD=CD，利用邻边相等的平行四边形是菱形进行证明即可．
试题解析：∵AB=CD，BC=AD，∴四边形ABCD是平行四边形，∴AB∥CD，∴∠BAE=∠DCF．又∵AE=CF，∴△ABE≌△CDF（SAS），∴AB=CD，∵AB∥CD，∴四边形ABCD是平行四边形，∵AC平分∠BAD，∴∠BAE=∠DAF，∵∠BAE=∠DCF，∴∠DAF=∠DCF，∴AD=CD，∴四边形ABCD是菱形．
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
