题目内容
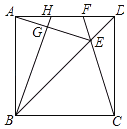
【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=AD,连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:①AH=DF;②∠AEF=45°;③S四边形EFHG=S△DEF+S△AGH;④BH平分∠ABE.其中不正确的结论有( )
A. 1个B. 2个C. 3个D. 4个
【答案】A
【解析】
先判断出∠DAE=∠ABH,再判断△ADE≌△CDE得出∠DAE=∠DCE=22.5°,∠ABH=∠DCF,再判断出Rt△ABH≌Rt△DCF从而得到①正确,根据三角形的外角求出∠AEF=45°,得出②正确;连接HE,判断出S△EFH≠S△EFD得出③错误,根据三角形的内角和和角平分线的定义得到④正确.
解:∵BD是正方形ABCD的对角线,
∴∠ABE=∠ADE=∠CDE=45°,AB=BC,
∵BE=BC,
∴AB=BE,
∵BG⊥AE,
∴BH是线段AE的垂直平分线,∠ABH=∠DBH=22.5°,
在Rt△ABH中,∠AHB=90°﹣∠ABH=67.5°,
∵∠AGH=90°,
∴∠DAE=∠ABH=22.5°,
在△ADE和△CDE中, ,
,
∴△ADE≌△CDE(SAS),
∴∠DAE=∠DCE=22.5°,
∴∠ABH=∠DCF,
在△ABH和△DCF中,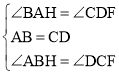 ,
,
∴△ABH≌△DCF(ASA),
∴AH=DF,∠CFD=∠AHB=67.5°,
∵∠CFD=∠EAF+∠AEF,
∴67.5°=22.5°+∠AEF,
∴∠AEF=45°,故①②正确;
如图,连接HE,
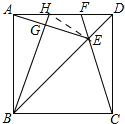
∵BH是AE垂直平分线,
∴AG=EG,
∴S△AGH=S△HEG,
∵AH=HE,
∴∠AHG=∠EHG=67.5°,
∴∠DHE=45°,
∵∠ADE=45°,
∴∠DEH=90°,∠DHE=∠HDE=45°,
∴EH=ED,
∴△DEH是等腰直角三角形,
∵EF不垂直DH,
∴FH≠FD,
∴S△EFH≠S△EFD,
∴S四边形EFHG=S△HEG+S△EFH=S△AHG+S△EFH≠S△DEF+S△AGH,故③错误,
∵∠AHG=67.5°,
∴∠ABH=22.5°,
∵∠ABD=45°,
∴∠ABH![]()
∴BH平分∠ABE,故④正确;
故选:A.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案