题目内容
在平面直角坐标系中,直线y=-
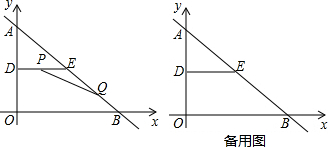
x+6与x轴、y轴分别交于点B、A,点D、E分别是AO、AB的中点,连接DE,点P从点D出发,沿DE方向匀速运动,速度为1cm/s;与此同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(s)(0<t<4).解答下列问题:
(1)分别写出点P和Q坐标(用含t的代数式表示);
(2)①当点Q在BE之间运动时,设五边形PQBOD的面积为y(cm2),
求y与t之间的函数关系式;
②在①的情况下,是否存在某一时刻t,使PQ分四边形BODE两部分的面积之比为S△PQE:S五边形PQBOD=1:29?若存在,求出此时t的值;若不存在,请说明理由;
(3)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,当t为何值时,⊙P能与△ABO的一边相切?
| 3 |
| 4 |
(1)分别写出点P和Q坐标(用含t的代数式表示);
(2)①当点Q在BE之间运动时,设五边形PQBOD的面积为y(cm2),
求y与t之间的函数关系式;
②在①的情况下,是否存在某一时刻t,使PQ分四边形BODE两部分的面积之比为S△PQE:S五边形PQBOD=1:29?若存在,求出此时t的值;若不存在,请说明理由;
(3)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,当t为何值时,⊙P能与△ABO的一边相切?

考点:一次函数综合题
专题:压轴题
分析:(1)利用直线的解析式首先求得直线与两坐标轴的交点坐标,然后利用三角形的中位线定理求得点P的纵坐标和点P的横坐标即可;
(2)①由P作PH⊥AB得到△PHE∽△AOB,利用相似三角形对应边的比相等表示出PH,然后根据三角形的面积公式求解即可;
②利用S△PQE:S五边形PQBOD=1:29列出方程求得t值即可.
(3)分当⊙P与OB相切时、当⊙P与OA相切时和当⊙P与AB相切时三种情况分类讨论得到答案.
(2)①由P作PH⊥AB得到△PHE∽△AOB,利用相似三角形对应边的比相等表示出PH,然后根据三角形的面积公式求解即可;
②利用S△PQE:S五边形PQBOD=1:29列出方程求得t值即可.
(3)分当⊙P与OB相切时、当⊙P与OA相切时和当⊙P与AB相切时三种情况分类讨论得到答案.
解答: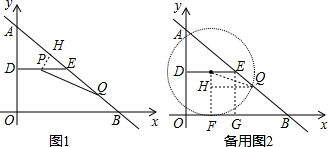 (1)∵直线y=-
(1)∵直线y=-
x+6与x轴、y轴分别交于点B、A,
∴点A的坐标为(0,6)
∵点D、E分别是AO、AB的中点,
∴DE∥x轴,
∴OD=3,
∵点P从点D出发,沿DE方向匀速运动,速度为1cm/s;
∴P(t,3),Q(8-
t,
t);
(2)①如图1,由P作PH⊥AB
△PHE∽△AOB
=
∴
=
∴PH=
(4-t)
S△PEQ
S四边形DOBE=
(4+8)×3=18y=18-(
t2-
t+6)=-
t2+
t+12
②
t2-
t+6=
×18
解得t=-
(舍),t=2
(3)当⊙P与OB相切时,
分别过点P、Q作PF、QG垂直于x轴,垂足为F、G,
再过点Q作QH⊥PF于点H,
如图2构造直角△PHQ,
此时,△BQG∽△BAO,BQ=2t,
得QG=HF=
t,BG=
t,
在Rt△PHQ中,PH2+HQ2=PQ2,
得(3-
t)2+(8-t-
t)2=32,
解得:t1=4(舍),t2=
当⊙P与OA相切时,
分别过点P、Q作PF、QG垂直于x轴,垂足为F、G,
再过点Q作QH⊥PF于点H,
如图3构造直角△PHQ,
此时,△BQG∽△BAO,BQ=2t,
得QG=HF=
t,BG=
t,
在Rt△PHQ中,PH2+HQ2=PQ2,
得(3-
t)2+(8-t-
t)2=t2,
解得:t1=
>4(舍),t2=
当⊙P与AB相切时,如图4,
此时,PE=4-t,EQ=2t-5,
由△EPQ∽△BAO,得
=
,
∴
=
,
解得:t=
∴当t=
,
,
时,⊙P可与△ABC的一边相切.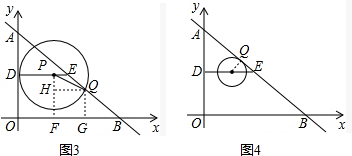
 (1)∵直线y=-
(1)∵直线y=-| 3 |
| 4 |
∴点A的坐标为(0,6)
∵点D、E分别是AO、AB的中点,
∴DE∥x轴,
∴OD=3,
∵点P从点D出发,沿DE方向匀速运动,速度为1cm/s;
∴P(t,3),Q(8-
| 8 |
| 5 |
| 6 |
| 5 |
(2)①如图1,由P作PH⊥AB
△PHE∽△AOB
| PH |
| AO |
| PE |
| AB |
| PH |
| 6 |
| 4-t |
| 10 |
∴PH=
| 3 |
| 5 |
S△PEQ
|
S四边形DOBE=
| 1 |
| 2 |
| 3 |
| 5 |
| 39 |
| 10 |
| 3 |
| 5 |
| 39 |
| 10 |
②
| 3 |
| 5 |
| 39 |
| 10 |
| 1 |
| 30 |
解得t=-
| 9 |
| 2 |
(3)当⊙P与OB相切时,
分别过点P、Q作PF、QG垂直于x轴,垂足为F、G,
再过点Q作QH⊥PF于点H,
如图2构造直角△PHQ,
此时,△BQG∽△BAO,BQ=2t,
得QG=HF=
| 6 |
| 5 |
| 8 |
| 5 |
在Rt△PHQ中,PH2+HQ2=PQ2,
得(3-
| 6 |
| 5 |
| 8 |
| 5 |
解得:t1=4(舍),t2=
| 80 |
| 41 |
当⊙P与OA相切时,
分别过点P、Q作PF、QG垂直于x轴,垂足为F、G,
再过点Q作QH⊥PF于点H,
如图3构造直角△PHQ,
此时,△BQG∽△BAO,BQ=2t,
得QG=HF=
| 6 |
| 5 |
| 8 |
| 5 |
在Rt△PHQ中,PH2+HQ2=PQ2,
得(3-
| 6 |
| 5 |
| 8 |
| 5 |
解得:t1=
61+2
| ||
| 18 |
61-2
| ||
| 18 |
当⊙P与AB相切时,如图4,
此时,PE=4-t,EQ=2t-5,
由△EPQ∽△BAO,得
. |
| BO |
| EP |
| AB |
∴
| 2t-5 |
| 8 |
| 4-t |
| 10 |
解得:t=
| 41 |
| 14 |
∴当t=
| 80 |
| 41 |
61-2
| ||
| 18 |
| 41 |
| 14 |

点评:本题考查了一次函数的综合知识,特别是本题中涉及到的分类讨论思想更是中考中的热点考题之一,也是个重点内容,需重点训练.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
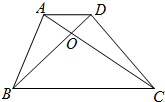 王大爷家有一块梯形形状土地,如图,AD∥BC,对角线AD,BC相交于点O,王大爷量得AD长3米,BC长9米,王大爷准备在△AOD处种大白菜,那么王大爷种大白菜的面积与整个土地的面积比为( )
王大爷家有一块梯形形状土地,如图,AD∥BC,对角线AD,BC相交于点O,王大爷量得AD长3米,BC长9米,王大爷准备在△AOD处种大白菜,那么王大爷种大白菜的面积与整个土地的面积比为( )| A、1:14 | B、3:14 |
| C、1:16 | D、3:16 |
根式
的值是( )
| 52 |
| A、5 | B、-5 | C、±5 | D、25 |
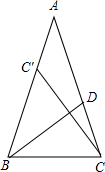 如图,D是△ABC的AC边上一点,AB=AC,BD=BC,将△BCD沿BD折叠,顶点C恰好落在AB边的C′处,则∠A′的大小是( )
如图,D是△ABC的AC边上一点,AB=AC,BD=BC,将△BCD沿BD折叠,顶点C恰好落在AB边的C′处,则∠A′的大小是( )| A、40° | B、36° |
| C、32° | D、30° |
下列函数中,y是x的二次函数的是( )
| A、y=x(2x-1)-2x2 | ||
B、y=
| ||
| C、y2=x-1 | ||
| D、y=2x2 |
 小新在镜子里看到墙上挂钟的时刻如图所示,则此时的实际时刻是
小新在镜子里看到墙上挂钟的时刻如图所示,则此时的实际时刻是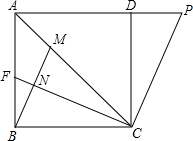 已知正方形ABCD如图所示,连接其对角线AC,∠BCA的平分线CF交AB于点F,过点B作BM⊥CF于点N,交AC于点M,过点C作CP⊥CF,交AD延长线于点P.
已知正方形ABCD如图所示,连接其对角线AC,∠BCA的平分线CF交AB于点F,过点B作BM⊥CF于点N,交AC于点M,过点C作CP⊥CF,交AD延长线于点P.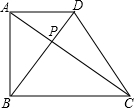 如图,梯形ABCD中,AD∥BC,AB⊥BC,对角线AC⊥BD于P,已知AD:BC=3:4,则BD:AC的值是
如图,梯形ABCD中,AD∥BC,AB⊥BC,对角线AC⊥BD于P,已知AD:BC=3:4,则BD:AC的值是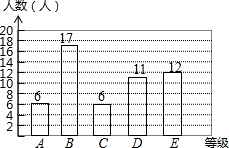 初三一班同学体育测试后,老师将全班同学成绩绘制成如图所示的条形统计图.每个等级成绩的人数的众数是
初三一班同学体育测试后,老师将全班同学成绩绘制成如图所示的条形统计图.每个等级成绩的人数的众数是