ĢāÄæÄŚČŻ
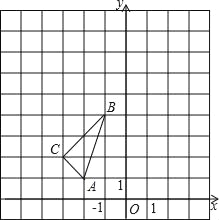
”¾ĢāÄæ”æŹżÖįÉĻµćA±ķŹ¾µÄŹżĪŖ10£¬µćM£¬N·Ö±šŅŌĆæĆėaøöµ„Ī»³¤¶Č£¬ĆæĆėbøöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲŹżÖįŌĖ¶Æ£¬a, bĀś×ć|a-5|+(b-6)2=0.
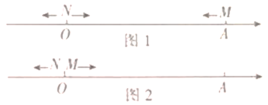
(1)ĒėÕę½ÓÓė³öa= , b= £»
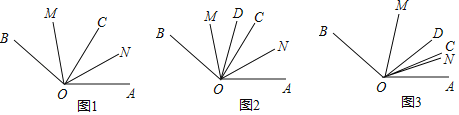
(2)ČēĶ¼1,µćM“ÓA³ö·¢ŃŲŹżÖįĻņ×óŌĖ¶Æ£¬µ½“ļŌµćŗóĮ¢¼“·µ»ŲĻņÓŅŌĖ¶Æ:Ķ¬Ź±µćN“ÓŌµć0³ö·¢ŃŲŹżÖįĻņ×óŌĖ¶Æ£¬ŌĖ¶ÆŹ±¼äĪŖt,µćPĪŖĻ߶ĪONµÄÖŠµćČōMP=MA,ĒótµÄÖµ:
(3)ČēĶ¼2,ČōµćM“ÓŌµćĻņÓŅŌĖ¶Æ£¬Ķ¬Ź±µćN“ÓŌµćĻņ×óŌĖ¶Æ£¬ŌĖ¶ÆŹ±¼äĪŖtŹ±MŌĖ¶Æµ½µćAµÄÓŅ²ą£¬Čō“ĖŹ±ŅŌM£¬N, O, AĪŖ¶ĖµćµÄĖłÓŠĻ߶ĪµÄ³¤¶ČŗĶĪŖ142,Ēó“ĖŹ±µćM¶ŌÓ¦µÄŹż.
”¾“š°ø”æ(1) 5,6 ;(2) ![]() »ņ
»ņ![]() £»(3) M¶ŌÓ¦µÄŹżĪŖ20.
£»(3) M¶ŌÓ¦µÄŹżĪŖ20.
”¾½āĪö”æ
(1)ÖŠøł¾Ż·ĒøŗŹżµÄŠŌÖŹ¼“æÉµĆ½ā£»
£Ø2£©·ÖČżÖÖĒéæö£¬·Ö±š±ķŹ¾MPŗĶMA£¬øł¾ŻMP=MAĮŠ³ö·½³Ģ£¬½ā·½³Ģ¼“æɣ؊č×¢Ņāt£¾0£©£»
£Ø3£©ŅĄ¾ŻĢāŅā»³öĶ¼ŠĪ£¬øł¾ŻĶ¼ŠĪæÉÖŖMN= NO+ OM=11t.M£¬N, O, AĪŖ¶ĖµćµÄĖłÓŠĻ߶ĪµÄ³¤¶ČŗĶĪŖ3MN+OA=142£¬½«MN=11t“śČė£¬¼“æÉĒó³ötµÄÖµ£¬Mµć±ķŹ¾µÄŹżæÉĒó.
½ā£ŗ£Ø1£©”ß|a-5|+£Øb-6£©2=0£®
”ąa-5=0£¬b-6=0
”ąa=5£¬b=6
¹ŹŅĄ“ĪĢī£ŗ5,6£»
£Ø2£©¢ŁµćMĪ“µ½“ļOŹ±£Ø0£¼t”Ü2Ź±£©£¬
NP=OP=3t£¬AM=5t£¬OM=10-5t£¬MP=3t+10-5t
¼“3t+10-5t=5t£¬½āµĆ![]() £¬
£¬
¢ŚµćMµ½“ļO·µ»Ų£¬Ī“µ½“ļAµć»ņøÕµ½“ļAµćŹ±£¬¼“µ±£Ø2£¼t”Ü4Ź±£©£¬
OM=5t-10£¬AM=20-5t, MP=3t+5t-10
¼“3t+5t-10=20-5t£¬½āµĆ![]()
¢ŪµćMµ½“ļO·µ»ŲŹ±£¬ŌŚAµćÓŅ²ą£¬¼“t£¾4Ź±
OM=5t-10£¬AM=5t-20£¬MP=3t+5t-10,
¼“3t+5t-10=5t-20£¬½āµĆ![]() £Ø²»·ūŗĻĢāŅāÉįČ„£©.
£Ø²»·ūŗĻĢāŅāÉįČ„£©.
×ŪÉĻ![]() »ņ
»ņ![]() £»
£»
£Ø3£©ČēĻĀĶ¼£ŗ

øł¾ŻĢāŅā£ŗNO=6t£¬OM=5t£¬ĖłŅŌMN=6t+5t=11t
ŅĄĢāŅā£ŗ NO+OA+AM+AN+OM+MN=MN+MN+OA+MN=33t+10=142£¬
½āµĆt=4.“ĖŹ±M¶ŌÓ¦µÄŹżĪŖ20.

 ÓÅѧĆūŹ¦ĆūĢāĻµĮŠ“š°ø
ÓÅѧĆūŹ¦ĆūĢāĻµĮŠ“š°ø