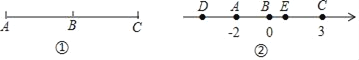题目内容
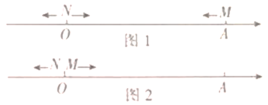
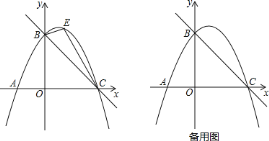
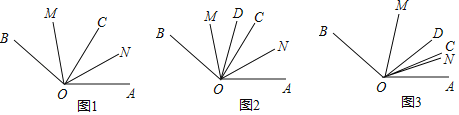
【题目】已知:∠AOB=140°,OC,OM,ON是∠AOB内的射线.
(1)如图1所示,若OM平分∠BOC,ON平分∠AOC,求∠MON的度数:
(2)如图2所示,OD也是∠AOB内的射线,∠COD=15°,ON平分∠AOD,OM平分∠BOC.当∠COD绕点O在∠AOB内旋转时,∠MON的位置也会变化但大小保持不变,请求出∠MON的大小;
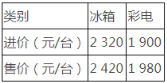
(3)在(2)的条件下,以∠AOC=20°为起始位置(如图3),当∠COD在∠AOB内绕点O以每秒3°的速度逆时针旋转t秒,若∠AON:∠BOM=19:12,求t的值.
【答案】(1)∠MON的度数为70°.(2)∠MON的度数为62.5°.(3)t的值为20.
【解析】
(1)根据角平分线的性质以及角的和差倍关系转化求出角的度数;
(2)根据角平分线的性质可以求得:∠MON=![]() (∠AOB+∠COD)﹣∠COD,代入数据即可求得;
(∠AOB+∠COD)﹣∠COD,代入数据即可求得;
(3)由题意得∠AON=![]() (20°+3t+15°),∠BOM=
(20°+3t+15°),∠BOM=![]() (140°﹣20°﹣3t),由此列出方程即可求解.
(140°﹣20°﹣3t),由此列出方程即可求解.
(1)∵ON平分∠AOC,OM平分∠BOC,
∴∠CON=![]() ∠AOC,∠COM=
∠AOC,∠COM=![]() ∠BOC
∠BOC
∠MON=∠CON+∠COM
=![]() (∠AOC+∠BOC)
(∠AOC+∠BOC)
=![]() ∠AOB
∠AOB
又∠AOB=140°
∴∠MON=70°
答:∠MON的度数为70°.
(2)∵OM平分∠BOC,ON平分∠AOD,
∴∠COM=![]() ∠BOC,∠DON=
∠BOC,∠DON=![]() ∠AOD
∠AOD
即∠MON=∠COM+∠DON﹣∠COD
=![]() ∠BOC+
∠BOC+![]() ∠AOD﹣∠COD
∠AOD﹣∠COD
=![]() (∠BOC+∠AOD)﹣∠COD.
(∠BOC+∠AOD)﹣∠COD.
=![]() (∠BOC+∠AOC+∠COD)﹣∠COD
(∠BOC+∠AOC+∠COD)﹣∠COD
=![]() (∠AOB+∠COD)﹣∠COD
(∠AOB+∠COD)﹣∠COD
=![]() (140°+15°)﹣15°
(140°+15°)﹣15°
=62.5°
答:∠MON的度数为62.5°.
(3)∠AON=![]() (20°+3t+15°),
(20°+3t+15°),
∠BOM=![]() (140°﹣20°﹣3t)
(140°﹣20°﹣3t)
又∠AON:∠BOM=19:12,
12(35°+3t)=19(120°﹣3t)
得t=20
答:t的值为20.