Question

【题目】阅读下面材料：

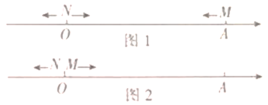
小明遇到这样一个问题：如图1，在中和中，，连接交于点.求证：.

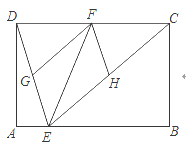
小明经探究发现，过点作，交于点（如图2），从而可证，使问题得到解决.

（1）请你按照小明单独探究思路，完成他的证明过程；

参考小明思考问题的方法，解决下面的问题：

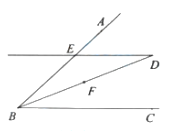
（2）如图3，在与中，分别为、的中线，连接并延长交于点，是否存在与相等的线段？若存在，请找出并证明；若不存在，说明理由.

Answer 1

【答案】（1）见解析；（2）存在，，见解析.

【解析】

（1）根据余角的性质得到∠3=∠4，根据“AAS”证明,由全等三角形的性质得到BG=DF，∠5=∠6，根据等腰三角形的判定即可得到结论；

（2）点作，交的延长线于点，先根据“SAS”证明，从而，再根据“AAS”证明，可得，再根据等腰三角形的判定即可得证.

（1）明：（1）如图2所示，

∵，

∴.

∵，

∴.

∵，

∴.

∴，.

∴，

∴.

∴.

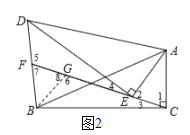
（2）如图3，.

过点作，交的延长线于点，

∵、分别为、的中线，

∴.

∵,

∴.

∴.

∵，

∴.

∵，

∴.

∴.

∴.

∴.

∵，

∴.

∴.

∴.