题目内容
【题目】如图所示，甲乙两点沿着边长为3cm的正方形，按A→B→C→D→A…的方向行走，甲从A点以3cm/s的速度、乙从B点以a cm/s的速度同时行走，设运动时间为t秒，t=2时甲乙两点第一次相遇.
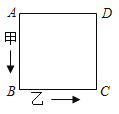
（1）求a
（2）若a＞3，且甲乙第一次相遇后，乙的速度变为5cm/s，当两点第二次相遇前相距4cm时，t为多少？
【答案】（1）
cm/s；（2）4秒；
【解析】
（1）根据追击问题列出关于a的方程解答即可；
（2）第一次相遇后，同时出发，第二次相遇前4m，即为乙追上甲的路程关系，列出方程解答即可.
解：（1）由题意得：3×2=2a+3，解得：a=；
所以a=cm/s
（2）设运动时间为t秒，
根据题意得：5t=3t+4×3-4，
解得：t=4
所以当两点第二次相遇前相距4cm时，t为4秒.
练习册系列答案
相关题目
【题目】某校组织了有奖征文活动，并设立了一、二、三等奖.根据设奖情况买了
件奖品，其中二等奖件数比一等奖件数的
倍少
件，各种奖品的单价如表所示:
一等奖 | 二等奖 | 三等奖 | |
单价/元 |
|
|
|
数量/件 |
|
如果计划一等奖买
件
(1)请把表填完整(填化简后的结果) .
(2)请用含有的代数式表示买件的总费用(写出解答过程并化简).
(3)若一等奖买件，则共花费多少元?
