题目内容
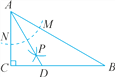
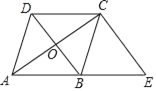
【题目】如图,已知菱形ABCD的对角线AC,BD相交于点O,过C作CE⊥AC,交AB的延长线于点E.
(1)求证:四边形BECD是平行四边形;
(2)若∠E=50°,求∠DAB的度数.
【答案】(1)证明见解析;(2)∠DAB=80°.
【解析】
![]() 直接利用菱形的性质对角线互相垂直,得出
直接利用菱形的性质对角线互相垂直,得出![]() ,进而得出答案;
,进而得出答案;![]() 利用菱形、平行四边形的性质得出
利用菱形、平行四边形的性质得出![]() ,进而利用三角形内角和定理得出答案.
,进而利用三角形内角和定理得出答案.
(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,DC∥BE,
又∵CE⊥AC,
∴BD∥EC,
∴四边形BECD是平行四边形;
(2)解:∵四边形ABCD是菱形,
∴AD=AB,
∴∠ADB=∠ABD,
∵四边形BECD是平行四边形,
∴DB∥CE,
∴∠CEA=∠DBA=50°,
∴∠ADB=50°,
∴∠DAB=180°﹣50°﹣50°=80°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目