Question

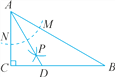
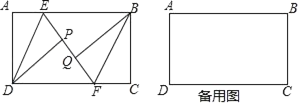
【题目】如图，在矩形ABCD中，AD＝4，E，F分别为边AB，CD上一动点，AE＝CF，分别以DE，BF为对称轴翻折△ADE，△BCF，点A，C的对称点分别为P，Q．若点P，Q，E，F恰好在同一直线上，且PQ＝1，则EF的长为_____．

Answer 1

【答案】5或

【解析】

过点E作，垂足为G，首先证明为等腰三角形，然后设，然后分两种情况求解：I.当QF与PE不重叠时，由翻折的性质可得到，则， II. 当QF与PE重叠时，：EF＝DF＝2x﹣1，FG＝x﹣1，然后在中，依据勾股定理列方程求解即可．

解：I.当QF与PE不重叠时，如图所示：过点E作EG⊥DC，垂足为G．

设AE＝FC＝x．

由翻折的性质可知：∠AED＝∠DEP，EP＝AE＝FC＝QF＝x，则EF＝2x+1．

∵AE∥DG，

∴∠AED＝∠EDF．

∴∠DEP＝∠EDF．

∴EF＝DF．

∴GF＝DF﹣DG＝x+1．

在Rt△EGF中，EF2＝EG2+GF2，即(2x+1)2＝42+(x+1)2，解得：x＝2(负值已舍去)．

∴EF＝2x+1＝2×2+1＝5．

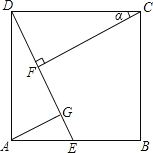
II. 当QF与PE重叠时，备用图中，同法可得：EF＝DF＝2x﹣1，FG＝x﹣1，

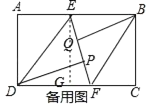
在Rt△EFG中，∵EF2＝EG2+FG2，

∴(2x﹣1)2＝42+(x﹣1)2，

∴x＝或﹣2(舍弃)，

∴EF＝2x﹣1＝

故答案为：5或．