��Ŀ����
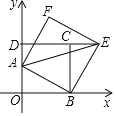
����Ŀ����ͼ1��ʾ����ƽ��ֱ������ϵ�У���A��y���������ϣ���B��C�ֱ���x��ĸ����ᡢ�������ϣ���AB��AC����ACB��30�㣬OD��AB�ڵ�D��
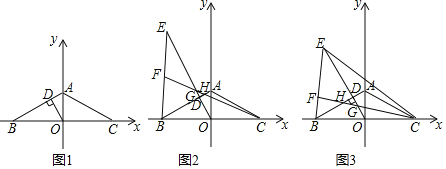
��1����֤��BD��3AD��
��2����ͼ2����E��OD���ӳ����ϣ�����BE�����߶�BE��ȡ��F������CF�ֱ�OE��AB�ڵ�G��H����G��H��D�����غϣ�����FE��FG����֤����EBA����BCF�Ķ���Ϊ��ֵ��
��3����ͼ3���ڣ�2���������£�����EC����C��4![]() ��0����A��0��4������S��ECG��
��0����A��0��4������S��ECG��
���𰸡���1������������2������������3��S��EGC��12![]() .
.
��������
��1������ֱ���������е������Ҷ������ɵõ�BD��AD�ij��ȹ�ϵ.��2�����������ε��ڽǺ�ʽ���ɵá�EBA����BCF��30��.��3����BΪԲ�ģ�BO��Ϊ�뾶������ED�ڵ�M������BM������C��EO�Ĵ��ߣ���EO���ӳ����ڵ�N���ٸ���ȫ�����������ʣ��ɵ�S��EGC.
�⣺��1����AB��AC����ACB��30�㣬OD��AB
���ABC��30�㣬��ODB��90�㣬
���BOD��60�㣬
���AOD��30�㣬
��AD��![]() OA��OA��
OA��OA��![]() AB
AB
��OA��2AD��AB��2AO��
��AB��4AD��
��BD��3AD��
��2����FE��FG��
�����E����EGF������
���OGC������
�ߡ�DOB��60�㣬
���BCF��60������
�ߡ�EDB��90�㣬
���EBA��90�㩁����
���EBA����BCF��30�㣬
���EBA����BCF�Ķ���Ϊ��ֵ��
��3����ͼ1��ʾ����BΪԲ�ģ�BO��Ϊ�뾶������ED�ڵ�M������BM������C��EO�Ĵ��ߣ���EO���ӳ����ڵ�N��
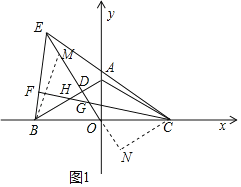
��BM��OC����EMB����GOC��120�㣬
�ߡ�BEM����OGC��
���EMB�ա�GOC��AAS����
��EM��OG��
��EG��MO��BO��4![]() ��
��
�ߡ�CON��60�㣬��N��90�㣬
���OCN��30�㣬
��ON��![]() OC��2
OC��2![]() ��
��
��CN��6��
��S��EGC��EGCN![]() ��4
��4![]() ��6��
��6��![]() ��12
��12![]() ��
��