题目内容
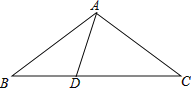
【题目】如图,![]() 中,
中,![]() 是
是![]() 的平分线.若
的平分线.若![]() 分别是
分别是![]() 和
和![]() 上的动点,则
上的动点,则![]() 的最小值是_________.
的最小值是_________.

【答案】![]()
【解析】
如图,作点Q关于直线BD的对称点Q′,作AM⊥BC于M,由PA+PQ=PA+PQ′,根据垂线段最短可知当A、P、Q′共线,且与AM重合时,PA+PQ的值最小,为线段AM的长,根据三角形的面积求出AM的长即可得.
如图,作AM⊥BC于M,
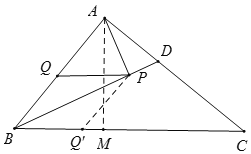
因为BD平分∠ABC,所以作点Q关于直线BD的对称点Q′,连接PQ′,
∴PQ=PQ′,
∴PA+PQ=PA+PQ′,
∴当A、P、Q′共线时,PA+PQ的值最小,
根据垂线段最短可知A、P、Q′共线且与AM重合时取得最小值,
即PA+PQ的最小值为线段AM的长,
∵△ABC中,∠BAC=90°,AB=3,BC=5,CA=4,
S△ABC=![]() ,
,
∴![]() ,
,
∴AM=![]() ,
,
∴PA+PQ的最小值为![]() ,
,
故答案为:![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目