题目内容
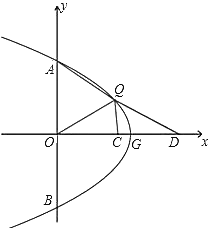
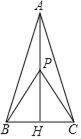
【题目】如图,△ABC中,∠BAC=30°且AB=AC,P是底边上的高AH上一点.若AP+BP+CP的最小值为2![]() ,则BC=_____.
,则BC=_____.
【答案】![]()
【解析】
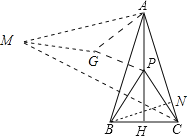
如图将△ABP绕点A顺时针旋转60°得到△AMG.连接PG,CM.首先证明当M,G,P,C共线时,PA+PB+PC的值最小,最小值为线段CM的长,想办法求出AC的长即可解决问题.
如图将△ABP绕点A顺时针旋转60°得到△AMG.连接PG,CM.
∵AB=AC,AH⊥BC,
∴∠BAP=∠CAP,
∵PA=PA,
∴△BAP≌△CAP(SAS),
∴PC=PB,
∵MG=PB,AG=AP,∠GAP=60°,
∴△GAP是等边三角形,
∴PA=PG,
∴PA+PB+PC=CP+PG+GM,
∴当M,G,P,C共线时,PA+PB+PC的值最小,最小值为线段CM的长,
∵AP+BP+CP的最小值为2![]() ,
,
∴CM=2![]() ,
,
∵∠BAM=60°,∠BAC=30°,
∴∠MAC=90°,
∴AM=AC=2,
作BN⊥AC于N.则BN=![]() AB=1,AN=
AB=1,AN=![]() ,CN=2-
,CN=2-![]() ,
,
∴BC=![]() .
.
故答案为![]() .
.

练习册系列答案
相关题目
【题目】已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
x | -1 | 0 | 1 | 3 |
y | -3 | 1 | 3 | 1 |
下列结论:①抛物线的开口向下;②其图象的对称轴为x=1;③当x<1时,函数值y随x的增大而增大;④方程ax2+bx+c=0有一个根大于4,其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个