题目内容
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)题中的抛物线上有一个动点P,当点P在抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标;
(3)设(1)题中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.

【答案】(1)解析式为y=x2﹣2x﹣3;(2)点P的坐标为(2![]() +1,4),(﹣2
+1,4),(﹣2![]() +1,4),(1,﹣4);(3)存在, Q点坐标为(1,﹣2).
+1,4),(1,﹣4);(3)存在, Q点坐标为(1,﹣2).
【解析】(1)∵抛物线y=x2+bx+c与![]() 轴的两个交点分别为A(-1,0),B(3,0)
轴的两个交点分别为A(-1,0),B(3,0)
∴![]() ┄ 2分
┄ 2分
解之,得![]() ┄ 3分
┄ 3分
∴所求抛物线的解析式为:y=x2-2x-3 ┄ 4分
(2)设点P的坐标为(x,y),由题意,得
S△ABC=![]() ×4×|y|=8 ┄ 5分
×4×|y|=8 ┄ 5分
∴|y|=4, ∴ y=±4 ┄ 6分
当y=4时, x2-2x-3=4 ∴ x1=1+![]() , x2=1-
, x2=1-![]() ┄ 7分
┄ 7分
当y=-4时,x2-2x-3=-4 ∴ x=1 ┄ 8分
∴当P点的坐标分别为![]() 、
、![]() 、(1,-4)时,S△PAB="8." ┄ 9分
、(1,-4)时,S△PAB="8." ┄ 9分
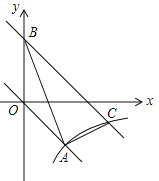
(3) 解法1: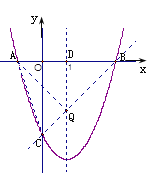
在抛物线y=x2-2x-3的对称轴上存在点Q, 使得ΔQAC的周长最小. ┄ 10分
∵AC长为定值,∴要使ΔQAC的周长最小,只需QA+QC最小.
∵点A关于对称轴x=1的对称点是B(3,0),
抛物线y=x2-2x-3与y轴交点C的坐标为(0,-3)
∴由几何知识可知,Q是直线BC与对称轴x=1的交点 ┄ 11分
设直线BC的解析式为y=kx-3.
∵直线BC过点B(3,0) ∴ 3k-3=0 ∴ k=1.
∴直线BC的解析式为 y=x-3 ┄ 12分
∴当x=1时,y=-2.
∴点Q的坐标为(1,-2). ┄ 13分
(3) 解法2:
在抛物线y=x2-2x-3的对称轴上存在点Q ,使得ΔQAC的周长最小. ┄ 10分
∵AC长为定值,∴要使ΔQAC的周长最小,只需QA+QC最小
∵点A关于对称轴x=1的对称点是B(3,0),
抛物线y=x2-2x-3与y轴交点C的坐标为(0,-3)
∴由几何知识可知,Q是直线BC与对称轴x=1的交点. ┄ 11分
∵OC∥DQ,
∴ΔBDQ∽ΔBOC.
∴![]() ,即
,即![]() . ┄ 12分
. ┄ 12分
∴DQ=2. ∴点Q的坐标为(1,-2). ┄ 13分
(1)已知了抛物线过B、C两点,而抛物线的解析式中也只有两个待定系数,因此可将B、C的坐标代入抛物线的解析式中,即可求出待定系数的值,也就出了二次函数的解析式.
(2)根据(1)中得出的抛物线的解析式,可求得A点的坐标,也就能得出AB的长.△PAB中,AB的长为定值,那么可根据△PAB的面积求出P到AB的距离,即P点纵坐标的绝对值,然后将其代入抛物线的解析式中(分正负两个值)即可求出P点的坐标.
(3)本题的关键是找出Q点的位置,已知了B与A点关于抛物线的对称轴对称,因此只需连接BC,直线BC与对称轴的交点即为Q点.可根据B、C两点的坐标先求出直线BC的解析式,然后联立抛物线对称轴的解析式即可求出Q点的坐标.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案