Question

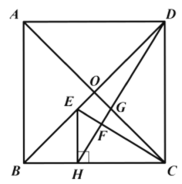
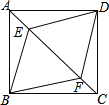
【题目】如图，有两张矩形纸片ABCD和EFGH，AB＝EF＝2cm，BC＝FG＝8cm．把纸片ABCD交叉叠放在纸片EFGH上，使重叠部分为平行四边形，且点D与点G重合．当两张纸片交叉所成的角α最小时，sinα等于（　　）

A.B.C.D.

Answer 1

【答案】B

【解析】

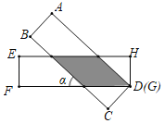
由“ASA”可证△CDM≌△HDN，可证MD=DN，即可证四边形DNKM是菱形，当点B与点E重合时，两张纸片交叉所成的角a最小，可求DM=，即可求的值．

解：如图，

∵∠ADC=∠HDF=90°
∴∠CDM=∠NDH，且CD=DH，∠H=∠C=90°
∴△CDM≌△HDN（ASA）
∴MD=ND，且四边形DNKM是平行四边形
∴四边形DNKM是菱形
∴KM=DM
∵sinα=sin∠DMC=，
∴当点B与点E重合时，两张纸片交叉所成的角a最小，
设MD=a=BM，则CM=8-a，
∵MD2=CD2+MC2，
∴a2=4+（8-a）2，
∴a=，
∴DM=，

∴；

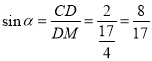故选：B．