题目内容
如图1,小红将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得AB=15,AD=12.在进行如下操作时遇到了下面的几个问题,请你帮助解决.
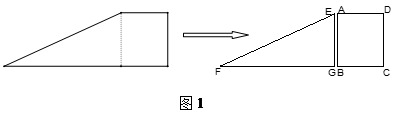
(1)将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2)求FB的长度
(2)在(1)的条件下,小红想用△EFG包裹矩形ABCD,她想了两种包裹的方法如图3、图4,请问哪种包裹纸片的方法使得未包裹住的面积大?(纸片厚度忽略不计)请你通过计算说服小红。
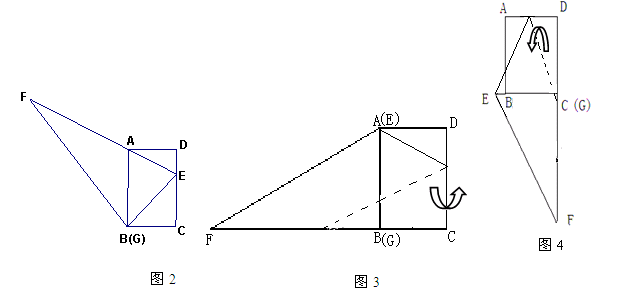

(1)将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2)求FB的长度
(2)在(1)的条件下,小红想用△EFG包裹矩形ABCD,她想了两种包裹的方法如图3、图4,请问哪种包裹纸片的方法使得未包裹住的面积大?(纸片厚度忽略不计)请你通过计算说服小红。

(1)30;(2) 二种包裹纸片的方法使得未包裹住的面积相等.
试题分析:(1)利用矩形的性质以及得出△ADE∽△FBE,求出即可;
(2)根据Rt△F,HN~Rt△F,EG,得到HN=3,从而S△AMH=144;由Rt△GBE~Rt△C,B,G,得到GB,=24,从而S△B,C,G=144,进行比较即可.
⑴BE=AD=15,在RtBCE中,CE2="B" E2-BC2=152-122,求得CE=9,DE=6,
证Rt△ADE~Rt△FBE,
求得BF="30"
⑵①如图1,将矩形ABCD和Rt△FBE以CD为轴翻折,则△AMH即为未包裹住的面积,
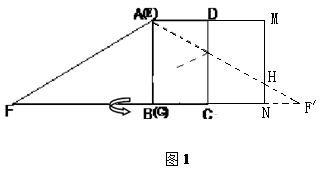
由Rt△F,HN~Rt△F,EG,得到HN=3,
从而S△AMH=144
②如图2,将矩形ABCD和Rt△ECF以AD为轴翻折,由Rt△GBE~Rt△C,B,G,得到GB,=24,
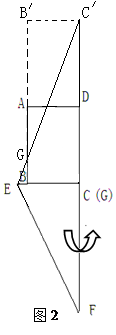
从而S△B,C,G=144,∴未包裹的面积为144.
∴按照二种包裹的方法未包裹的面积相等。

练习册系列答案
相关题目


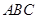 和
和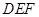 叠放在一起,使三角板
叠放在一起,使三角板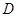 与三角板
与三角板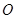 重合,其中
重合,其中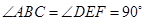 ,
,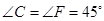 ,
,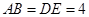 ,把三角板
,把三角板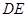 与射线
与射线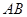 相交于点
相交于点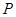 ,射线
,射线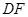 与线段
与线段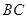 相交于点
相交于点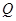 .
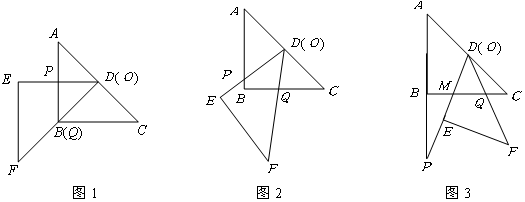
.
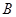 ,即点
,即点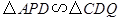 .此时,
.此时,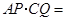 ;将三角板
;将三角板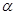 .其中
.其中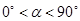 ,问
,问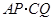 的值是否改变?答: (填“会”或“不会”);若改变,
的值是否改变?答: (填“会”或“不会”);若改变,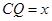 ,两块三角板重叠面积为
,两块三角板重叠面积为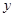 ,求
,求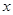 的函数关系式.(图2,图3供解题用)
的函数关系式.(图2,图3供解题用)




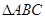 纸片中,已知
纸片中,已知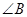 =
=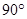 ,AB=6,,BC=8,折叠纸片使AB边与AC边重合,B点落在点E上,折痕为AD,则BD的长为( )
,AB=6,,BC=8,折叠纸片使AB边与AC边重合,B点落在点E上,折痕为AD,则BD的长为( ) 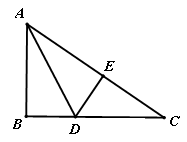
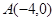 ,将其绕原点顺时针旋转60°,则点
,将其绕原点顺时针旋转60°,则点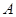 的对应点坐标为____________.
的对应点坐标为____________.