题目内容
【题目】将正整数 1 至 2024 按一定规律排列成如图所示的 8 列,规定从上到下依次为第 1 行,第 2 行,第 3 行,…从左往右依次为第 1 列至第 8 列.
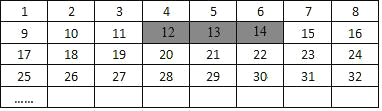
(1)数 56 在第 行 列 ;
(2)平移图中带阴影的方框,使方框框住相邻的三个数,若被框住的三个数中最大的一个数为 x,则被框的三个数的和能否等于 2019?若能,请求出 x;若不能,请说明理由.
【答案】(1)7,8;(2)不可能.
【解析】
(1)求出56÷8的商和余数即可求解;
(2)①①设被框住的三个数中,最大的一个数为x,则另外两个数为x﹣2,x﹣1,求和即可.②把2019代入①得到的三个数的和中的代数式,计算可得x的值;
(1)∵56÷8=7,
∴数56在第7行8列.
故答案为:7,8.
(2)①设被框住的三个数中,最大的一个数为x,则另外两个数为x﹣2,x﹣1,
∴三个数之和为x﹣2+x﹣1+x=3x﹣3.
②根据题意得:
3x﹣3=2019,
解得:x=674,
∵674=84×8+2,
∴数674在第85行2列,不符合题意,
∴三个数的和不可以等于2019.

【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
时间x(天) | 1≤x<9 | 9≤x<15 | x≥15 |
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 | |
销量(斤) | 80﹣3x | 120﹣x | |
储存和损耗费用(元) | 40+3x | 3x2﹣64x+400 | |
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?