题目内容
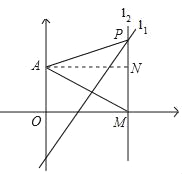
【题目】在平面直角坐标系中,点A(0,2),在x轴上任取一点M,连接AM,作AM的垂直平分线l1.过点M作x轴的垂线l2,l1与l2交于点P.设P点的坐标为(x,y).
(Ⅰ)当M的坐标取(3,0)时,点P的坐标为 ;
(Ⅱ)求x,y满足的关系式;
(Ⅲ)是否存在点M,使得△MPA恰为等边三角形?若存在,求点M的坐标;若不存在,说明理由.
【答案】(Ⅰ)(3,![]() );(Ⅱ)x,y满足的关系式是y=
);(Ⅱ)x,y满足的关系式是y=![]() x2+1;(Ⅲ)△MPA为等边三角形时,点M的坐标为(2
x2+1;(Ⅲ)△MPA为等边三角形时,点M的坐标为(2![]() ,0)或(﹣2
,0)或(﹣2![]() ,0).
,0).
【解析】分析:(Ⅰ)作AN⊥PM于N,根据线段垂直平分线的性质得到PA=PM,根据勾股定理计算;
(Ⅱ)分点M在x轴的正半轴上、点M在x轴的负半轴上两种情况,根据勾股定理列式计算;
(Ⅲ)由(Ⅰ)可知,PA=PM,设点M的坐标为(0,x),根据勾股定理列方程求出x的值.
详解:(Ⅰ)作AN⊥PM于N,
则四边形AOMN是矩形,
∴AN=OM=3,MN=OA=2,
∵l1是AM的垂直平分线,
∴PA=PM,
在Rt△APN中,AN2+PN2=AP2,即32+(y﹣2)2=y2,
解得,y=![]() ,
,
∴点P的坐标为(3,![]() ),
),
故答案为:(3,![]() );
);
(Ⅱ)当点M在x轴的正半轴上时,
在Rt△APN中,AN2+PN2=AP2,即x2+(y﹣2)2=y2,
解得,y=![]() x2+1,
x2+1,
同理,当点M在x轴的负半轴上时,x,y满足的关系式是y=![]() x2+1,
x2+1,
∴x,y满足的关系式是y=![]() x2+1;
x2+1;
(Ⅲ)由(Ⅰ)可知,PA=PM,
要使△MPA为等边三角形,只需MA=MP即可,
∵点A的坐标为(0,2),点M的坐标为(0,x),
∴AM=![]() ,
,
则![]() x2+1=
x2+1=![]() ,
,
解得,x=±2![]() ,
,
∴△MPA为等边三角形时,点M的坐标为(2![]() ,0)或(﹣2
,0)或(﹣2![]() ,0).
,0).

 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案【题目】鞋号是指鞋子的大小,中国于60年代后期,在全国测量脚长的基础上制定了“中国鞋号”,1998年政府发布了基于![]() 系统,用毫米做单位的中华人民共和国国家标准
系统,用毫米做单位的中华人民共和国国家标准![]() ,被称为“新鞋号”,之前以厘米为单位的鞋号从此被称为“旧鞋号”.新旧鞋号部分对应表如下:
,被称为“新鞋号”,之前以厘米为单位的鞋号从此被称为“旧鞋号”.新旧鞋号部分对应表如下:
新鞋号 | 220 | 225 | 230 | 235 | … | 270 |
旧鞋号 | 34 | 35 | 36 | 37 | … |
|
(1)![]() 的值为______;
的值为______;
(2)若新鞋号为![]() ,旧鞋号为
,旧鞋号为![]() ,则把旧鞋号转换为新鞋号的公式为______
,则把旧鞋号转换为新鞋号的公式为______