题目内容
在平面直角坐标系中, 抛物线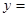
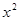 +
+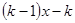 与直线
与直线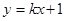 交于A, B两点,点A在点B的左侧.
交于A, B两点,点A在点B的左侧.
(1)如图1,当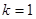 时,直接写出A,B两点的坐标;
时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
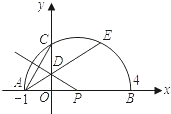
(3)如图2,抛物线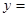
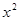 +
+ 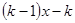
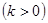 与
与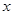 轴交于C,D两点(点C在点D的左侧).在直线
轴交于C,D两点(点C在点D的左侧).在直线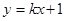 上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时
上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时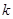 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.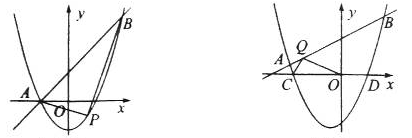
图1 图2
(1)A(-1,0) ,B(2,3)
(2)△ABP最大面积s= ; P(
; P(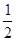 ,-
,- )
)
(3)存在;k=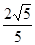
解析试题分析:(1)将两个解析式联立组成方程组,解方程组即得
要想△ABP的面积最大,则要在要求的抛物线上找到一个点P,使点P到直线AB的距离最大,这时过点P且与AB平行的直线与抛物线只有一个交点,利用根的判别式可确定平移后所得直线的解析式,进而可得点的坐标,求出面积
设圆心为E,连接EQ,直线与x轴交点为H,与y轴交点为F;由已知可得直线与两坐标轴交点的坐标,从而可得直线与坐标轴交点到原点的距离;由圆的切线及相似的知识可得出EQ、QH的长,
再由勾股定理可得要求的值
试题解析:(1)A(-1,0) ,B(2,3)
(2)平移直线AB得到直线L,当L与抛物线只有一个交点时,△ABP面积最大[如图12-1(1)]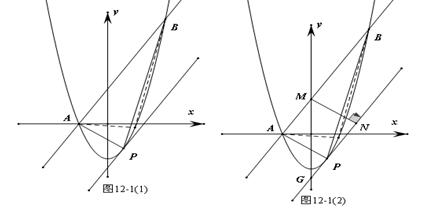
设直线L解析式为: ,
,
根据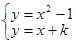 ,得
,得
判别式△ ,解得,
,解得,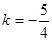
代入原方程中,得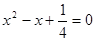 ;解得,
;解得, ,
, 
∴P(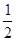 ,
,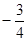 )
)
易求,AB交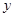 轴于M(0,1),直线L交轴
轴于M(0,1),直线L交轴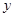 于G(0,
于G(0,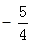 )
)
过M作MN⊥直线L于N,∵OM=1,OA=1,∴∠AMO=45°
∵∠AMN=90,∴∠NMO=45°
在RT△MNE中,∠NMO=45°,MG=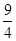 ,[如图12-1(2)]
,[如图12-1(2)]
∴ MN=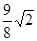 ,MN即为△ABP的高
,MN即为△ABP的高
由两点间距离公式,求得:AB=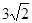
故△ABP最大面积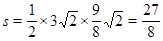
(3)设在直线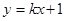 上存在唯一一点Q使得∠OQC=90°
上存在唯一一点Q使得∠OQC=90°
则点Q为以OC的中点E为圆心,OC为直径形成的圆E与直线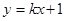 相切时的切点,[如图12-2(1)]
相切时的切点,[如图12-2(1)]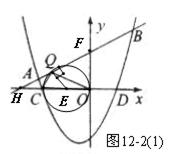
由解析式可知:C(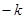 ,0),OC=
,0),OC=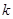 ,则圆E的半径:OE=CE=
,则圆E的半径:OE=CE=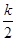 =QE
=QE
设直线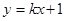 与
与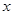 、
、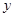 轴交于H点和F点,则F(0,1),∴OF=1 则H(
轴交于H点和F点,则F(0,1),∴OF=1 则H(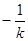 ,0), ∴OH =
,0), ∴OH =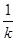
∴ EH=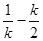
∵AB为切线 ∴EQ⊥AB,∠EQH=90°
在△FOH和△EQH中 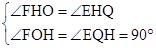
∴△FOH∽△EQH
∴ ∴ 1:
∴ 1: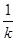 =
=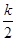 :QH,∴QH =
:QH,∴QH =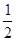
在RT△EQH中,EH=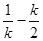 ,QH =
,QH =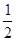 ,QE =
,QE =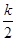 ,根据勾股定理得,
,根据勾股定理得,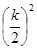 +
+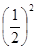 =
=
求得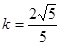
考点:1、平面直角坐标系中的平行与垂直;2、二次函数;3、一元二次方程根的判别式;4、圆(相切、圆心角)

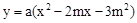 (其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.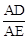 为定值;
为定值;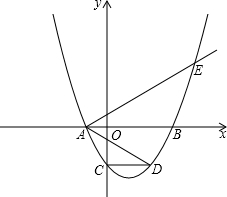
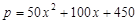 ,每处理一吨再生资源得到的新产品的售价定为100元.若该单位每月再生资源处理量为y(吨),每月的利润为w(元).
,每处理一吨再生资源得到的新产品的售价定为100元.若该单位每月再生资源处理量为y(吨),每月的利润为w(元).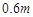 %.四月份,该单位得到国家科委的技术支持,使月处理成本比二月份的降低了
%.四月份,该单位得到国家科委的技术支持,使月处理成本比二月份的降低了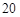 %.如果该单位四月份在保持三月份的再生资源处理量和新产品售价的基础上,其利润比二月份的利润减少了60元,求m的值.
%.如果该单位四月份在保持三月份的再生资源处理量和新产品售价的基础上,其利润比二月份的利润减少了60元,求m的值. ,其图像抛物线交
,其图像抛物线交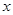 轴的于点A(1,0)、B(3,0),交y轴于点C.直线
轴的于点A(1,0)、B(3,0),交y轴于点C.直线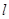 过点C,且交抛物线于另一点E(点E不与点A、B重合).
过点C,且交抛物线于另一点E(点E不与点A、B重合).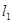 经过抛物线顶点D,交
经过抛物线顶点D,交
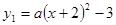 与
与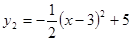 交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①
交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①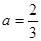 ;②
;②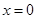 时,
时,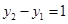 ;③平行于x轴的直线
;③平行于x轴的直线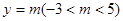 与两条抛物线有四个交点;④2AB=3AC.其中错误结论的个数是( )
与两条抛物线有四个交点;④2AB=3AC.其中错误结论的个数是( )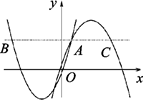
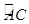 与
与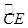 相等吗?请证明你的结论;
相等吗?请证明你的结论;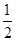 AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.