题目内容
已知二次函数 ,其图像抛物线交
,其图像抛物线交 轴的于点A(1,0)、B(3,0),交y轴于点C.直线
轴的于点A(1,0)、B(3,0),交y轴于点C.直线 过点C,且交抛物线于另一点E(点E不与点A、B重合).
过点C,且交抛物线于另一点E(点E不与点A、B重合).
(1)求此二次函数关系式;
(2)若直线 经过抛物线顶点D,交
经过抛物线顶点D,交 轴于点F,且
轴于点F,且 ∥
∥ ,则以点C、D、E、F为顶点的四边形能否为平行四边形?若能,求出点E的坐标;若不能,请说明理由.
,则以点C、D、E、F为顶点的四边形能否为平行四边形?若能,求出点E的坐标;若不能,请说明理由.
(3)若过点A作AG⊥ 轴,交直线
轴,交直线 于点G,连OG、BE,试证明OG∥BE.
于点G,连OG、BE,试证明OG∥BE.
(1)此二次函数关系式为:y=x2-4x+3;
(2)以点C、D、E、F为顶点的四边形能成为平行四边形;点E的坐标为(2+ ,2),(2-
,2),(2- ,2),(2+
,2),(2+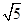 ,4),(2-
,4),(2-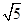 ,4).
,4).
(3)证明见解析.
解析试题分析:(1)由二次函数y=x2+bx+c,其图象抛物线交x轴于点A(1,0),B(3,0),直接利用待定系数法求解即可;
(2)以点C、D、E、F为顶点的四边形构成平行四边形,有两种情形,分类讨论即可;
(3)先过点E作EH⊥x轴于点H,设直线CE的解析式为:y=kx+3,然后分别求得点G与E的坐标,即可证得△OAG∽△BHE,则可得∠AOG=∠HBE,即可.
试题解析:(1)∵二次函数y=x2+bx+c,图象交x轴于点A(1,0),B(3,0),
∴ ,
,
解得: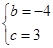 ,
,
∴此二次函数关系式为:y=x2-4x+3;
(2)当CD为平行四边形对角线时,过点D作DM⊥AB于点M,过点E作EN⊥OC于点N,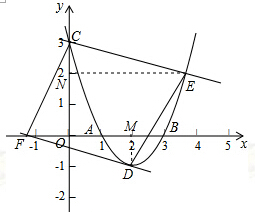
∵y=x2-4x+3=(x-2)2-1,
∴点D(2,-1),点C(0,3),
∴DM=1,
∵l1∥l,
∴当CE=DF时,四边形CEDF是平行四边形,
∴∠ECF+∠CFD=180°,
∵∠OCF+∠OFC=90°,
∴∠ECN+∠DFM=90°,
∵∠DFM+∠FDM=90°,
∴∠ECN=∠FDM,
在△ECN和△FDM中, ,
,
∴△ECN≌△FDM(AAS),
∴CN=DM=1,
∴ON=OC-CN=3-1=2,
当y=2时,x2-4x+3=2,
解得:x=2± ,
,
∴点E(2+ ,2)或(2-
,2)或(2- ,2);
,2);
当CD为平行四边形一条边时,
则EF∥CD,且EF=CD.
过点D作DM⊥y轴于点M,则DM=2,OM=1,CM=OM+OC=4;
过点E作EN⊥x轴于点N.
易证△CDM≌△EFN,∴EN=CM=4.
∴x2-4x+3=4,
解得:x=2±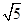 .
.
综上所述,以点C、D、E、F为顶点的四边形能成为平行四边形;点E的坐标为(2+ ,2),(2-
,2),(2- ,2),(2+
,2),(2+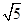 ,4),(2-
,4),(2-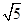 ,4).
,4).
(3)如图,过点E作EH⊥x轴于点H,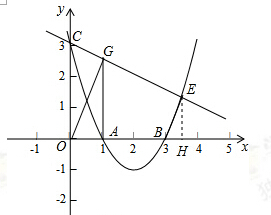
设直线CE的解析式为:y=kx+3,
∵A(1,0),AG⊥x轴,
∴点G(1,k+3),
即OA=1,AG=k+3,
∵E是直线与抛物线的交点,
∴ ,
,
解得: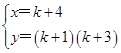 ,
,
∴点E(k+4,(k+1)(k+3)),
∴BH=OH-OB=k+3,EH=(k+1)(k+3),
∴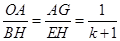 ,
,
∵∠OAG=∠BHE=90°,
∴△OAG∽△BHE,
∴∠AOG=∠HBE,
∴OG∥BE.
考点:二次函数综合题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案某商品现在的售价为每件35元.每天可卖出50件.市场调查反映:如果调整价格.每降价1元,每天可多卖出2件.请你帮助分析,当每件商品降价多少元时,可使每天的销售额最大,最大销售额是多少?
设每件商品降价x元.每天的销售额为y元.
(1)分析:根据问题中的数量关系.用含x的式子填表:
| | 原价 | 每件降价1元 | 每件降价2元 | … | 每件降价x元 |
| 每件售价(元) | 35 | 34 | 33 | … | |
| 每天售量(件) | 50 | 52 | 54 | … | |
(2)(由以上分析,用含x的式子表示y,并求出问题的解)

 )三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.
)三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.

 +
+ 与直线
与直线 交于A, B两点,点A在点B的左侧.
交于A, B两点,点A在点B的左侧.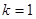 时,直接写出A,B两点的坐标;
时,直接写出A,B两点的坐标; 与
与 轴交于C,D两点(点C在点D的左侧).在直线
轴交于C,D两点(点C在点D的左侧).在直线 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 =
= ,求k;
,求k;
 x2+bx+c经过点B,且顶点在直线x=
x2+bx+c经过点B,且顶点在直线x= 上.
上.
 ,抛物线y = ax2+bx+2经过点A(m,0),B(2,0),D
,抛物线y = ax2+bx+2经过点A(m,0),B(2,0),D  三点.
三点.