题目内容
如图,在平面直角坐标系中,抛物线y=ax2+bx+4与x轴的一个交点为A(-2,0),与y轴的交点为C,对称轴是x=3,对称轴与x轴交于点B.
(1)求抛物线的函数表达式;
(2)经过B,C的直线l平移后与抛物线交于点M,与x轴交于点N,当以B,C,M,N为顶点的四边形是平行四边形时,求出点M的坐标;
(3)若点D在x轴上,在抛物线上是否存在点P,使得△PBD≌△PBC?若存在,直接写出点P的坐标;若不存在,请说明理由.
(1)抛物线为y=-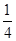 x2+
x2+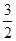 x+4.(2)M的坐标为(6,4)或(3-
x+4.(2)M的坐标为(6,4)或(3- ,-4)或(3+
,-4)或(3+ ,-4).(3)点P的坐标为(4+
,-4).(3)点P的坐标为(4+ ,
,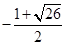 )或(4-
)或(4- ,
, )或(-1+
)或(-1+ ,-8+2
,-8+2 )或(-1-
)或(-1- ,-8-2
,-8-2 ).
).
解析试题分析:(1)解析式已存在,y=ax2+bx+4,我们只需要根据特点描述求出a,b即可.由对称轴为- ,又过点A(-2,0),所以函数表达式易得.
,又过点A(-2,0),所以函数表达式易得.
(2)四边形为平行四边形,则必定对边平行且相等.因为已知MN∥BC,所以MN=BC,即M、N的位置如B、C位置关系,则可分2种情形,①N点在M点右下方,即M向下平行4个单位,向右2个单位与N重合;②M点在N右下方,即N向下平行4个单位,向右2个单位与M重合.因为M在抛物线,可设坐标为(x,-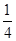 x2+
x2+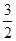 x+4),易得N坐标.由N在x轴上,所以其纵坐标为0,则可得关于x的方程,进而求出x,求出M的坐标.
x+4),易得N坐标.由N在x轴上,所以其纵坐标为0,则可得关于x的方程,进而求出x,求出M的坐标.
(3)使△PBD≌△PBC,易考虑∠CBD的平分线与抛物线的交点.确定平分线可因为BC=BD,可作等腰△BCD,利用三线合一,求其中线所在方程,进而与抛物线联立得方程组,解出P即可.
试题解析:(1)∵抛物线y=ax2+bx+4交x轴于A(-2,0),
∴0=4a-2b+4,
∵对称轴是x=3,
∴- =3,即6a+b=0,
=3,即6a+b=0,
两关于a、b的方程联立解得 a=-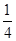 ,b=
,b=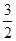 ,
,
∴抛物线为y=-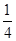 x2+
x2+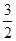 x+4.
x+4.
(2)∵四边形为平行四边形,且BC∥MN,
∴BC=MN.
①N点在M点右下方,即M向下平移4个单位,向右平移2个单位与N重合.
设M(x,-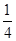 x2+
x2+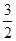 x+4),则N(x+2,-
x+4),则N(x+2,-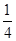 x2+
x2+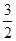 x),
x),
∵N在x轴上,
∴-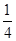 x2+
x2+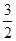 x=0,
x=0,
解得 x=0(M与C重合,舍去),或x=6,
∴xM=6,
∴M(6,4).
②M点在N右下方,即N向下平行4个单位,向右2个单位与M重合.
设M(x,- 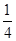 x2+
x2+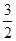 x+4),则N(x-2,-
x+4),则N(x-2,-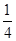 x2+
x2+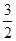 x+8),
x+8),
∵N在x轴上,
∴-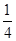 x2+
x2+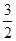 x+8=0,
x+8=0,
解得 x=3- ,或x=3+
,或x=3+ ,
,
∴xM=3- ,或3+
,或3+ .
.
∴M(3- ,-4)或(3+
,-4)或(3+ ,-4)
,-4)
综上所述,M的坐标为(6,4)或(3- ,-4)或(3+
,-4)或(3+ ,-4).
,-4).
(3)∵OC=4,OB=3,
∴BC=5.
如果△PBD≌△PBC,那么BD=BC=5,
∵D在x轴上,
∴D为(-2,0)或(8,0).
①当D为(-2,0)时,连接CD,过B作直线BE平分∠DBC交CD于E,交抛物线于P1,P2,
此时△P1BC≌△P1BD,△P2BC≌△P2BD,
∵BC=BD,
∴E为CD的中点,即E(-1,2),
设过E(-1,2),B(3,0)的直线为y=kx+b,则 ,
,
解得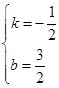 ,
,
∴BE:y=- x+
x+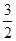 .
.
设P(x,y),则有 ,
,
解得  ,或
,或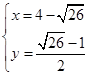 ,
,
则P1(4+ ,
,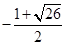 ),P2(4-
),P2(4- ,
, ).
).
②当D为(8,0)时,连接CD,过B作直线BF平分∠DBC交CD于F,交抛物线于P3,P4,
此时△P3BC≌△P3BD,△P4BC≌△P4BD,
∵BC=BD,
∴F为CD的中点,即E(4,2),
设过E(4,2),B(3,0)的直线为y=kx+b,则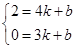 ,
,
解得 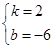 ,
,
∴BF:y=2x-6.
设P(x,y),则有 ,
,
解得 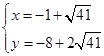 或
或 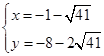 ,
,
则P3(-1+ ,-8+2
,-8+2 ),P4(-1-
),P4(-1- ,-8-2
,-8-2 ).
).
综上所述,点P的坐标为(4+ ,
,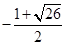 )或(4-
)或(4- ,
, )或(-1+
)或(-1+ ,-8+2
,-8+2 )或(-1-
)或(-1- ,-8-2
,-8-2 ).
).
【考点】二次函数综合题.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案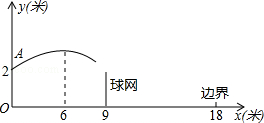


 +
+ 与直线
与直线 交于A, B两点,点A在点B的左侧.
交于A, B两点,点A在点B的左侧.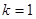 时,直接写出A,B两点的坐标;
时,直接写出A,B两点的坐标; 与
与 轴交于C,D两点(点C在点D的左侧).在直线
轴交于C,D两点(点C在点D的左侧).在直线 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 =
= ,求k;
,求k;
 与
与 重叠部分面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围;
重叠部分面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围; 是以DG为腰的等腰三角形?若存在,求出t的值;若不存在,说明理由.
是以DG为腰的等腰三角形?若存在,求出t的值;若不存在,说明理由.
 x2+bx+c经过点B,且顶点在直线x=
x2+bx+c经过点B,且顶点在直线x= 上.
上.
 的方程:
的方程: ①和
①和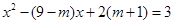 ②,其中
②,其中 .
. 的图象与
的图象与 、
、 两点(点
两点(点 处,点
处,点 处,若点
处,若点 的值;
的值; ,在(2)的条件下,函数
,在(2)的条件下,函数 ,
, 的图象位于直线
的图象位于直线 左侧的部分与直线
左侧的部分与直线 (
( )交于两点,当向上平移直线
)交于两点,当向上平移直线 的值是________________.
的值是________________.
