题目内容
【题目】如图,AB、CB、CD分别与⊙O切于E,F,G,且AB∥CD.连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.
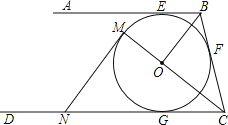
(1)当OB=6cm,OC=8cm时,求⊙O的半径;
(2)求证:MN=NG.
【答案】(1)⊙O的半径为4.8;(2)见解析.
【解析】
(1)根据切线的性质得到OB平分∠EBF,OC平分∠GCF,OF⊥BC,再根据平行线的性质得∠GCF+∠EBF=180°,则有∠OBC+∠OCB=90°,即∠BOC=90°;连接OF,则OF⊥BC,根据勾股定理就可以求出BC的长,然后根据△BOC的面积就可以求出⊙O的半径;
(2)根据切线的判定和性质定理即可得到结论.
(1)∵AB、BC、CD分别与⊙O切于E、F、G,
∴OB平分∠EBF,OC平分∠GCF,OF⊥BC,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠DCB,
∠DCB,
又∵AB∥CD,
∴∠GCF+∠EBF=180°,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°;,
连接OF,则OF⊥BC,
由(1)知,△BOC是直角三角形,
∴BC=![]() =10,
=10,
∵S△BOC=![]() OBOC=
OBOC=![]() BCOF,
BCOF,
∴6×8=10×OF,
∴OF=4.8,
∴⊙O的半径为4.8;
(2)证明:∵AB、BC、CD分别与⊙O切于点E、F、G,
∴∠OBC=![]() ∠ABC,∠DCB=2∠DCM,
∠ABC,∠DCB=2∠DCM,
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠OBC+∠OCB=![]() (∠ABC+∠DCB)=
(∠ABC+∠DCB)=![]() ×180°=90°,
×180°=90°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-90°=90°,
∵MN∥OB,
∴∠NMC=∠BOC=90°,
即MN⊥MC 且MO是⊙O的半径,
∴MN是⊙O的切线,
∴MN=NG.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目