Question

【题目】已知抛物线C：y1＝a（x﹣h）2﹣1，直线l：y2＝kx﹣kh﹣1．

（1）求证：直线l恒过抛物线C的顶点；

（2）当a＝﹣1，m≤x≤2时，y1≥x﹣3恒成立，求m的最小值；

（3）当0＜a≤2，k＞0时，若在直线l下方的抛物线C上至少存在两个横坐标为整数的点，求k的取值范围．

Answer 1

【答案】（1）见解析；（2）m的最小值为1；（3）k＞4．

【解析】

(1)由抛物线的解析式可知抛物线的顶点坐标为(h，-1)，然后证明点(h,-1)符合直线y2＝kx﹣kh﹣1的解析式即可;

(2)令,依据拋物线的解析式可得到拋物线的顶点在直线y=-1上，由m≤x≤2时，y1≥x－3恒成立可得到拋物线的顶点坐标为(2，-1)，然后找出抛物线y1＝a（x﹣h）2﹣1位于直线上方时自变量x的取值范围，从而可确定出m的最小值;

(3)由(1)可知抛物线C与直线l都过点A(h,-1).当0<a≤3时，k>0,在直线l下方的抛物线C上至少存在两个横坐标为整数点，即当x=h+2时，恒成立，然后由可得到关于k的不等式，从而可求得k:的取值范围.

（1）抛物线C的顶点坐标为（h，﹣1），

当x＝h时，y2＝kh﹣kh﹣1＝﹣1，

所以直线l恒过抛物线C的顶点；

（2）当a＝﹣1时，抛物线C解析式为y1＝﹣（x﹣h）2﹣1，

不妨令y3＝x﹣3

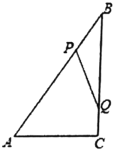
如图1所示：抛物线C的顶点在直线y＝﹣1上移动，

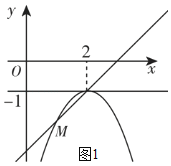
当m≤x≤2时，y1≥x﹣3恒成立，

则可知抛物线C的顶点为（2，﹣1），

设抛物线C与直线y3＝x﹣3除顶点外的另一交点为M，

此时点M的横坐标即为m的最小值，

由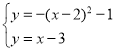，解得：x＝1，x＝2，

所以m的最小值为1．

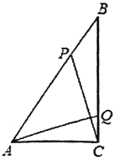
（3）如图2所示：由（1）可知：抛物线C与直线l都过点A（h，﹣1）．

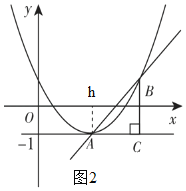
当0＜a≤2时，k＞0，在直线l下方的抛物线C上至少存在两个横坐标为整数点，即当x＝h+2时，y2＞y1恒成立．

所以k（h+2）﹣kh﹣1＞a（h+2﹣h）2﹣1，整理得：k＞2a．

又因为0＜a≤2，

所以0＜2a＜4，所以k＞4．