题目内容
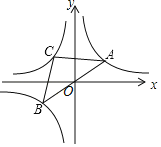
【题目】如图,把一块含有30°角的直角三角尺放置在平面直角坐标系中,BC边落在x轴的正半轴上,点A在第一象限内,∠ACB=90°,∠CAB=30°,AC=4![]() ,沿着AB翻折三角尺,直角顶点C落在C′处.设A、C′两点的横坐标分别为m、n.
,沿着AB翻折三角尺,直角顶点C落在C′处.设A、C′两点的横坐标分别为m、n.
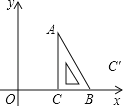
(1)试用m的代数式表示n;
(2)若反比例函数y=![]() (x>0)的图象恰好经过A、C′两点,求k的值.
(x>0)的图象恰好经过A、C′两点,求k的值.
【答案】(1)n=m+6;(2)k的值是24![]() .
.
【解析】
(1)过点C′作C′D⊥x轴于D,在Rt△ACB中和在Rt△C′DB中用三角函数求出相关线段长即可求解;
(2)将A、C′两点代入y=![]() 中,列含k,m的方程组即可求k值.
中,列含k,m的方程组即可求k值.
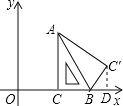
解:(1)如图,过点C′作C′D⊥x轴于D.
在Rt△ACB中,∠ACB=90°,∠CAB=30°,AC=4![]() ,
,
∴∠C′BA=∠CBA=60°,BC=BC′=ACtan30°=4,
∵∠C′BD=180°-60°-60°=60°,
在Rt△C′DB中,BD=BC′cos60°=2,C′D=BC′sin60°=2![]() ,
,
∵OD=OC+BC+BD,
∴n=m+4+2=m+6;
(2)∵反比例函数y=![]() (x>0)的图象恰好经过A、C′两点,
(x>0)的图象恰好经过A、C′两点,
∴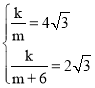 ,
,
解得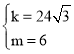 .
.
故k的值是24![]() .
.

练习册系列答案
相关题目