Question

【题目】如图，MN是⊙O的直径，MN=4，点A在⊙O上，∠AMN=30°，B为 的中点，P是直径MN上一动点．

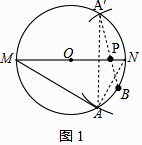
（1）利用尺规作图，确定当PA+PB最小时P点的位置（不写作法，但要保留作图痕迹）．
（2）求PA+PB的最小值．

Answer 1

【答案】
（1）

解：如图1所示，点P即为所求；

（2）

解：由（1）可知，PA+PB的最小值即为A′B的长，连接OA′、OB、OA，

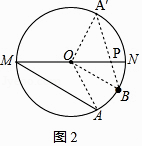
∵A′点为点A关直线MN的对称点，∠AMN=30°，

∴∠AON=∠A′ON=2∠AMN=2×30°=60°，

又∵B为 的中点，

∴ = ，

∴∠BON=∠AOB= ∠AON= ×60°=30°，

∴∠A′OB=∠A′ON+∠BON=60°+30°=90°，

又∵MN=4，

∴OA′=OB= MN= ×4=2，

∴Rt△A′OB中，A′B= =2 ，即PA+PB的最小值为2

【解析】（1）作点A关于MN的对称点A′，连接A′B，与MN的交点即为点P；（2）由（1）可知，PA+PB的最小值即为A′B的长，连接OA′、OB、OA，先求∠A′OB=∠A′ON+∠BON=60°+30°=90°，再根据勾股定理即可得出答案．
【考点精析】解答此题的关键在于理解圆周角定理的相关知识，掌握顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半，以及对轴对称-最短路线问题的理解，了解已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径．