Question

【题目】已知：在平面直角坐标系xOy中，一次函数y=kx+b（k≠0）的图象经过点A（4，0），C（0，﹣4），另有一点B（﹣2，0）．

（1）求一次函数解析式；
（2）联结BC，点P是反比例函数y= 的第一象限图象上一点，过点P作y轴的垂线PQ，垂足为Q．如果△QPO与△BCO相似，求P点坐标；
（3）联结AC，求∠ACB的正弦值．

Answer 1

【答案】
（1）

解：把A（4，0），C（0，﹣4）代入y=kx+b可得

，解得 ，

∴一次函数解析式为y=x﹣4

（2）

解：设P点坐标为（x， ），

∵，∠PQO=∠BOC=90°，

∴当△POQ和△BCO时是有∠BCO=∠POQ或∠BCO=∠OPQ，

①当∠BCO=∠POQ时，则tan∠BCO=tan∠POQ，

∴ = ，解得x=2 或x=﹣2 （舍去），

∴P点坐标为（2 ， ）；

②当∠BCO=∠OPQ时，则tan∠BCO=tan∠OPQ，

∴ = ，解得x= 或x=﹣ （舍去），

∴P点坐标为（ ，2 ）；

综上可得P点坐标为（2 ， ）或（ ，2 ）

（3）

解：作AD⊥BC交BC于D，如图，

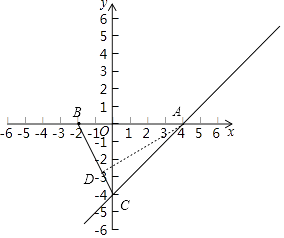
∵A（4，0），C（0，﹣4），B（﹣2，0），

∴AC=4 ，BC= =2

∵S△ABC= ABOC= BCAD，

∴6×4=2 AD，

∴AD ，

∴在Rt△ADC中，sin∠ACB= = =

【解析】（1）把A、C两点的坐标代入可求得一次函数解析式；（2）可设出P点坐标为（x， ），由△POQ和△BCO相似可知有两种情况，当∠BCO=∠POQ时，利用两角的正切值相等，可得到关于x的方程，可求得x的值，可得P点坐标；当∠BCO=∠OPQ时，同理可求得P点坐标；（3）作AD⊥BC于点D，由△ABC的面积可求得AD的长，且可求得AC的长，在Rt△ADC中，可求得∠ACB的正弦值．
【考点精析】关于本题考查的一次函数的性质和一次函数的图象和性质，需要了解一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小；一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远才能得出正确答案．