题目内容
定义:如图1,点C在线段AB上,若满足AC2=BC•AB,则称点C为线段AB的黄金分割点.
如图2,△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D.
(1)求证:点D是线段AC的黄金分割点;
(2)求出线段AD的长.
解:(1)∵∠A=36°,AB=AC,∴∠ABC=∠ACB=72°。
∵BD平分∠ABC,∴∠CBD=∠ABD=36°,∠BDC=72°。∴AD=BD,BC=BD。
∴△ABC∽△BDC。∴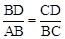 ,即
,即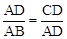 。∴AD2=AC•CD。
。∴AD2=AC•CD。
∴点D是线段AC的黄金分割点。
(2)由(1)AD2=AC•CD,即AD2=AC•(AC﹣AD),AD2=1﹣AD,AD2+AD﹣1=。
解得AD=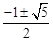 (舍去负值)。
(舍去负值)。
∴AD=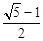 。
。
解析试题分析:(1)判断△ABC∽△BDC,根据对应边成比例可得出答案。
(2)根据(1)列出方程即可求出AD的长度。

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
如图所示的几何体的主视图是( )
A. | B. | C. | D. |


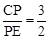 ,BP′=
,BP′= 时,求线段AB的长.
时,求线段AB的长.
 的值;
的值;
 (180°- ) =45°。 ∠BDM=45°(同理)。
(180°- ) =45°。 ∠BDM=45°(同理)。 ,
,

 ︰1,猜想BF︰FC= ;并证明你的结论
︰1,猜想BF︰FC= ;并证明你的结论 
