题目内容
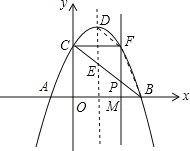
【题目】如图,抛物线![]() 与
与![]() 轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
(1)直接写出A、B、C三点的坐标和抛物线的对称轴;
(2)连接![]() ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作PF∥DE交抛物线于点F,设点P的横坐标为m;
作PF∥DE交抛物线于点F,设点P的横坐标为m;
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?
②设△BCF的面积为S,求S与m的函数关系式,S是否有最大值?如有,请求出最大值,没有请说明理由.


【答案】(1) A(1,0),B(3,0),C(0,3),抛物线对称轴为直线x=1 ;(2)①PF=m2+3m,m=2;②S=![]() ;当m=
;当m=![]() 时,S取得最大值为
时,S取得最大值为![]() .
.
【解析】试题分析:(1)已知了抛物线的解析式,当y=0时可求出A,B两点的坐标,当x=0时,可求出C点的坐标.根据对称轴x=![]() 可得出对称轴的解析式;(2)①根据B,C的坐标求出BC所在直线的解析式,然后将m分别代入直线BC和抛物线的解析式中,求得出两函数的值的差就是PF的长.根据直线BC的解析式,可得出E点的坐标,根据抛物线的解析式可求出D点的坐标,求出DE的长,然后让PF=DE,即可求出此时m的值.②根据△BCF的面积=△PFC的面积+△PFB的面积,即可求出关于S、m的函数关系式,利用二次函数的性质求得最大值即可.
可得出对称轴的解析式;(2)①根据B,C的坐标求出BC所在直线的解析式,然后将m分别代入直线BC和抛物线的解析式中,求得出两函数的值的差就是PF的长.根据直线BC的解析式,可得出E点的坐标,根据抛物线的解析式可求出D点的坐标,求出DE的长,然后让PF=DE,即可求出此时m的值.②根据△BCF的面积=△PFC的面积+△PFB的面积,即可求出关于S、m的函数关系式,利用二次函数的性质求得最大值即可.
试题解析:
(1)A(1,0),B(3,0),C(0,3),抛物线对称轴为直线x=1;
(2)①设直线BC的函数解析式为y=kx+b,
把B(3,0),C(0,3)分别代入得:
![]() ,
,
解得:k=1,b=3,
∴直线BC的解析式为y=x+3,
当x=1时,y=1+3=2,
∴E(1,2),
当x=m时,y=m+3,
∴P(m,m+3),
令y=x2+2x+3中x=1,得到y=4,∴D(1,4),
当x=m时,y=m2+2m+3,∴F(m,m2+2m+3),
∴线段DE=42=2,
∵0<m<3,∴线段PF=m2+2m+3(m+3)=m2+3m,
连接DF,由PF∥DE,得到当PF=DE时,四边形PEDF为平行四边形,
由m2+3m=2,得到m=2或m=1(不合题意,舍去),
则当m=2时,四边形PEDF为平行四边形;
②连接BF、CF,设直线PF与x轴交于点M,由B(3,0) ,O(0,0),
可得OB=OM+MB=3,
∵S=S△BPF+S△CPF=![]() PFBM+
PFBM+![]() PFOM=
PFOM=![]() PF(BM+OM)=
PF(BM+OM)= ![]() PFOB,
PFOB,
∴S=![]() ×3(m2+3m)=
×3(m2+3m)= ![]() m2+
m2+![]() m=
m=![]() (0<m<3),
(0<m<3),
则当m=![]() 时,S取得最大值为
时,S取得最大值为![]() .
.

 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案