题目内容
已知抛物线的顶点(-1,-4)且过点(0,-3),直线l是它的对称轴。
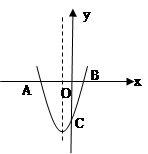
(1)求此抛物线的解析式;
(2)设抛物线交x轴于点A、B(A在B的左边),交y轴于点C,P为l上的一动点,当△PBC的周长最小时,求P点的坐标。
(3)在直线l上是否存在点M,使△MBC是等腰三角形,若存在,直接写出符合条件的点M的坐标;若不存在请说明理由。
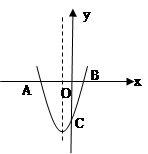
(1)求此抛物线的解析式;
(2)设抛物线交x轴于点A、B(A在B的左边),交y轴于点C,P为l上的一动点,当△PBC的周长最小时,求P点的坐标。
(3)在直线l上是否存在点M,使△MBC是等腰三角形,若存在,直接写出符合条件的点M的坐标;若不存在请说明理由。
(1)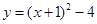 (2)
(2) (3)
(3)
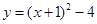 (2)
(2) (3)
(3)
试题分析:(1)抛物线的顶点(-1,-4),则设抛物线的顶点式为
 ,因为抛物线过点(0,-3),所以
,因为抛物线过点(0,-3),所以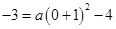 ,解得a=1,所以抛物线的解析式
,解得a=1,所以抛物线的解析式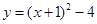
(2)由(1)知抛物线的解析式
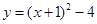
∵直线l是它的对称轴
∴它的对称轴x=-1
抛物线交x轴于点A、B(A在B的左边),令y=0,则
 ,解得x=-3,x=1,所以A点的坐标(-3,0),B点的坐标(1,0);抛物线交y轴于点C,令x=0,则
,解得x=-3,x=1,所以A点的坐标(-3,0),B点的坐标(1,0);抛物线交y轴于点C,令x=0,则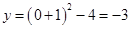 ,所以C点的坐标(0,-3);P为l上的一动点,当△PBC的周长=PB+PC+BC,因为BC的长度一定,所以要使△PBC的周长最小,即PB+PC最小,作点B关于对称轴的对称点,坐标为(-3,0),即是A点,设过A、C的直线为y=kx+b,则
,所以C点的坐标(0,-3);P为l上的一动点,当△PBC的周长=PB+PC+BC,因为BC的长度一定,所以要使△PBC的周长最小,即PB+PC最小,作点B关于对称轴的对称点,坐标为(-3,0),即是A点,设过A、C的直线为y=kx+b,则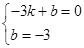
解得
 ,所以过点A、C的直线为y=x-3,则P点即为直线为y=x-3与对称轴的交点,解得
,所以过点A、C的直线为y=x-3,则P点即为直线为y=x-3与对称轴的交点,解得
(3)存在,)直线l为x=-1,它与X轴的交点为N(-1,0),由(2)知B点的坐标(1,0),所以它们两点是关于原点对称,此时这三点构成了等腰三角形,M点即为对称轴与X轴的交点,所以M的坐标(-1,0);当△MBC是等腰三角形,并以BC为△MBC的底边,设M的坐标为(-1,y);此时需满足MB=MC,而MB=
 ,MC=
,MC= ,解得y=-1,y=
,解得y=-1,y=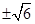 ,所以,当y=-1时M的坐标为
,所以,当y=-1时M的坐标为 ,当y=
,当y=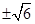 ,M的坐标为
,M的坐标为 ;综上所述满足条件的M的坐标为
;综上所述满足条件的M的坐标为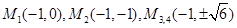
点评:本题考查抛物线,要求考生掌握抛物线的性质,会用待定系数法求抛物线的解析式,会求抛物线与坐标轴的交点坐标,以及对称轴

练习册系列答案
相关题目
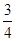 ,抛物线y=ax2+bx经过点A(4,0)与点(-2,6).
,抛物线y=ax2+bx经过点A(4,0)与点(-2,6).
 (吨)与月份
(吨)与月份 (
(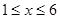 ,且
,且 (吨)与月份
(吨)与月份 ,且
,且 ,其图象如图所示.1至6月,污水厂处理每吨污水的费用
,其图象如图所示.1至6月,污水厂处理每吨污水的费用 (元)与月份
(元)与月份 ,该企业自身处理每吨污水的费用
,该企业自身处理每吨污水的费用 (元)与月份
(元)与月份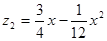 ;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
 与y轴正半轴交于点C,连接BC、AC,CD是⊙
与y轴正半轴交于点C,连接BC、AC,CD是⊙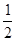 ,抛物线
,抛物线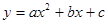 过A、B、C三点.
过A、B、C三点.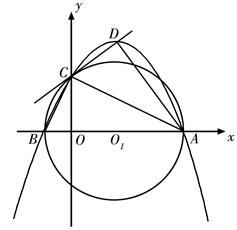
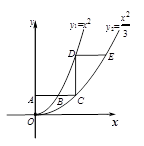
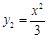 (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则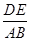 = .
= . 
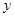 (克)与销售时间
(克)与销售时间 (月份)之间的函数图象. (4月份以30天计算)
(月份)之间的函数图象. (4月份以30天计算)
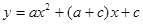 与一次函数
与一次函数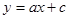 的大致图象,有且只有一个是正确的,正确的是
的大致图象,有且只有一个是正确的,正确的是
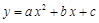 经过点(-1,0)和(3,0),那么它的对称轴是直线
经过点(-1,0)和(3,0),那么它的对称轴是直线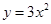 向左平移2个单位,所得抛物线的表达式为 .
向左平移2个单位,所得抛物线的表达式为 .