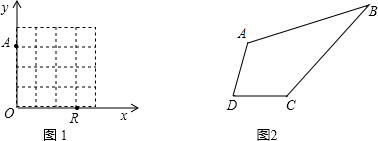题目内容
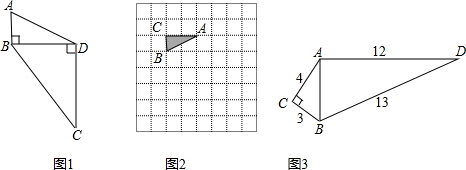
我们给出如下定义：如果一个直角三角形的斜边与另一个直角三角形的一边重合，且两个三角形不重叠，我们称这两个直角三角形是一对“伴侣三角形”，由这两个直角三角形拼成的四边形我们称为“美的四边形”．并且称这两个三角形重合的边为“美的四边形”的宽，另一条对角线叫“美的四边形”的长．解答下列问题：（1）判断图1是不是“美的四边形”？
（2）如图2，在8×8的正方形网格中，给定一个Rt△ABC，请你补上一个格点D，使以A、B、C、D为顶点的四边形是一个“美的四边形”（画出一个即可），并回答这样的点D共有几个？
（3）如图3，根据图中已知条件求“美的四边形”的长．（如有需要可使用562+482=5440）
分析：（1）根据题中的信息，验证是否符合即可，很明显图1不是．
（2）根据题中所给的定义，只要找到一个直角三角形，其中一边与AB重合即可，画出图形，知道可以画6个．
（3）根据定义即求BD的长度．
（2）根据题中所给的定义，只要找到一个直角三角形，其中一边与AB重合即可，画出图形，知道可以画6个．
（3）根据定义即求BD的长度．
解答：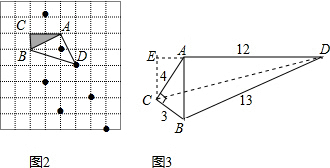
解：（1）两个直角边重合，不符合题中的信息．
所以图1不是“美的四边形”．
（2）符合要求的点有7个．
（3）如图3，作出辅助线CE⊥AD于E，交DA的延长线于E，
由∠BAD=90°得sin∠CAE=cos∠BAC=
，
∴CE=AC×sin∠CAE=4×
=
，
∴AE=AC×cos∠CAE=4×
=
，
∴DE=AE+AD=12+
=
，
∴CD=
=
故线段CD=
．
解：（1）两个直角边重合，不符合题中的信息．所以图1不是“美的四边形”．
（2）符合要求的点有7个．
（3）如图3，作出辅助线CE⊥AD于E，交DA的延长线于E，
由∠BAD=90°得sin∠CAE=cos∠BAC=
| 4 |
| 5 |
∴CE=AC×sin∠CAE=4×
| 4 |
| 5 |
| 16 |
| 5 |
∴AE=AC×cos∠CAE=4×
| 3 |
| 5 |
| 12 |
| 5 |
∴DE=AE+AD=12+
| 12 |
| 5 |
| 72 |
| 5 |
∴CD=
| DE2+CE2 |
| 8 |
| 5 |
| 85 |
故线段CD=
| 8 |
| 5 |
| 85 |
点评：本题是给出定义，根据定义求解的题，看似与课本知识无关，其实只不过是“换了件外衣”，同样要求有扎实的基础，在此基础上还考查理解分析能力．
练习册系列答案
名校课堂系列答案
相关题目
，M是平面直角坐标系内的点．
，则坐标平面内距离坐标为[p，q]时，点M可以有几个位置？并用三角尺在图③画出符合条件的点M（简要说明画法）．
