��Ŀ����
���Ǹ������¶��壺��ͼ�٣�ƽ��������ֱ��l1��l2�ཻ�ڵ�O������ƽ���ڵ�����һ��M����p��q�ֱ��ǵ�M��ֱ��l1��l2�ľ��루P��0��q��0����������Ǹ�ʵ����[p��q]�ǵ�M�ľ������꣮�����������壬�����������⣺
��ͼ�ڣ�ƽ��ֱ������ϵxoy�ڣ�ֱ��l1�Ĺ�ϵʽΪy=x��ֱ��l2�Ĺ�ϵʽΪy=
| 1 |
| 2 |
��1����p=q=0�����������Ϊ[0��0]ʱ����M�����ꣻ
��2����q=0����p+q=m��m��0��������ͼ�ڣ��ڵ�һ�����ڣ����������Ϊ[p��q]ʱ����M�����ꣻ
��3����p=1��q=
| 1 |
| 2 |

��������1����������ɵô�ʱM����ֱ�ߵĽ���λ�ã�
��2��������ɵô�ʱ��M��ֱ��l2�ϣ�����l2�Ľ���ʽ���M�����꣬�ٸ���k�ļ�������ɵó�M�����꣮
��3������ƽ���ߵ�֪ʶ���д��ʵĽ��
��2��������ɵô�ʱ��M��ֱ��l2�ϣ�����l2�Ľ���ʽ���M�����꣬�ٸ���k�ļ�������ɵó�M�����꣮
��3������ƽ���ߵ�֪ʶ���д��ʵĽ��
����⣺��1����p=q=0
���M��l1��l2�Ľ��㣬��M��0��0��
��2����q=0
���M��l2�ϣ�
��ͼ�ڣ��ڵ�һ������ȡ��M(a��
a)������M��MA��l1��l1�ڵ�A������M��BC��y��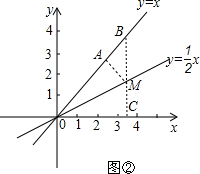 ��l1��x���ڵ�B��C
��l1��x���ڵ�B��C
��OC=BC
��q=0��p+q=m��m��0��
��p��0��
��MA=m��
�ߡ�B=45�㣬
��BM=
AM=
m��BC=BM+MC=
m+
a
��OC=BC��a=
m+
a�����a=2
m��
��M(2
m��
m)
��3����M��4��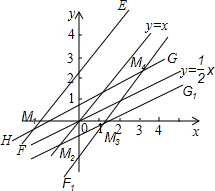
������
�ٷֱ����(0��
)��(0��-
)����ֱ��l1ƽ�е�ֱ��EF��E1F1����l1����Ϊ1��
�ڷֱ����(0��
)��(0��-
)����ֱ��l2ƽ�е�ֱ��GH��G1H1����l2����Ϊ
��
��ֱ��EF��E1F1��GH��G1H1��4������M1��M2��M3��M4���Ƿ��������ĵ㣮
���M��l1��l2�Ľ��㣬��M��0��0��
��2����q=0
���M��l2�ϣ�
��ͼ�ڣ��ڵ�һ������ȡ��M(a��
| 1 |
| 2 |
 ��l1��x���ڵ�B��C
��l1��x���ڵ�B��C��OC=BC
��q=0��p+q=m��m��0��
��p��0��
��MA=m��
�ߡ�B=45�㣬
��BM=
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
��OC=BC��a=
| 2 |
| 1 |
| 2 |
| 2 |
��M(2
| 2 |
| 2 |
��3����M��4��

������
�ٷֱ����(0��
| 2 |
| 2 |
�ڷֱ����(0��
| ||
| 4 |
| ||
| 4 |
| 1 |
| 2 |
��ֱ��EF��E1F1��GH��G1H1��4������M1��M2��M3��M4���Ƿ��������ĵ㣮
���������⿼����һ�κ�����֪ʶ���ۺ��Խ�ǿ���ѶȽϴ�ͬѧ��Ҫע��ϸ�ĵؽ�����ɵķ�����Ȼ�����������

��ϰ��ϵ�д�
 �ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
�ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
�����Ŀ

 ��M��ƽ��ֱ������ϵ�ڵĵ㣮
��M��ƽ��ֱ������ϵ�ڵĵ㣮 ��������ƽ���ھ�������Ϊ[p��q]ʱ����M�����м���λ�ã��������dz���ͼ�ۻ������������ĵ�M����Ҫ˵����������
��������ƽ���ھ�������Ϊ[p��q]ʱ����M�����м���λ�ã��������dz���ͼ�ۻ������������ĵ�M����Ҫ˵����������