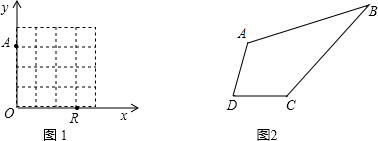题目内容
我们给出如下定义：如图2所示，若一个四边形的两组相邻两边分别相等，则称这个四边形为筝形四边形，把这两条相等的邻边称为这个四边形的筝边．
（1）写出一个你所学过的特殊四边形中是筝形四边形的图形的名称________；
（2）如图1，已知格点（小正方形的顶点）O（0，0），A（0，3），B（3，0），请你画出以格点为顶点，OA，OB为边的筝形四边OAMB；
（3）如图2，在筝形ABCD，AD=CD，AB=BC，若∠ADC=60°，∠ABC=30°，求证：2AB2=BD2
解：（1）∵正方形和菱形的角都为直角，且相邻两边分别相等，所以它们一定为筝形四边形；
（2）如图：
（3）证明：CB绕点C顺时针旋转60度至CE，连接BE，
∵BC=CE，∠BCE=60°，
∴△BCE为等边三角形，
∴∠BCE=60°，
∴△ABD≌△AEC，
∴BD=AE，
又∵∠ABC=30°，
∴∠ABE=90°，
∴△ABE为直角三角形，
∴AE2=BA2+BE2，
即：BD2=AE2=AB2+BE2=2AB2
∴2AB2=BD2．
分析：（1）从平时的积累中我们就可以很快想到，正方形和矩形符合．
（2）利用题目说明的四边形在坐标系中作出即可．
（3）然后根据图形作辅助线CE，看出△CBE为等边三角形，∠DCE为直角利用勾股定理进行解答即可．
点评：本题考查了勾股定理及全等三角形的判定及性质，此题关键为能够看出题中隐藏的全等三角形．
（2）如图：
（3）证明：CB绕点C顺时针旋转60度至CE，连接BE，
∵BC=CE，∠BCE=60°，
∴△BCE为等边三角形，
∴∠BCE=60°，
∴△ABD≌△AEC，
∴BD=AE，
又∵∠ABC=30°，
∴∠ABE=90°，
∴△ABE为直角三角形，
∴AE2=BA2+BE2，
即：BD2=AE2=AB2+BE2=2AB2
∴2AB2=BD2．
分析：（1）从平时的积累中我们就可以很快想到，正方形和矩形符合．
（2）利用题目说明的四边形在坐标系中作出即可．
（3）然后根据图形作辅助线CE，看出△CBE为等边三角形，∠DCE为直角利用勾股定理进行解答即可．
点评：本题考查了勾股定理及全等三角形的判定及性质，此题关键为能够看出题中隐藏的全等三角形．
练习册系列答案
相关题目
，M是平面直角坐标系内的点．
，则坐标平面内距离坐标为[p，q]时，点M可以有几个位置？并用三角尺在图③画出符合条件的点M（简要说明画法）．
