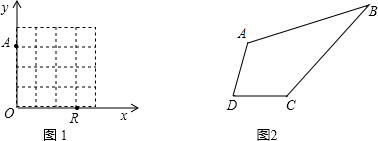题目内容
我们给出如下定义:如图①,平面内两条直线l1、l2相交于点O,对于平面内的任意一点M,若p、q分别是点M到直线l1和l2的距离(P≥0,q≥0),称有序非负实数对[p,q]是点M的距离坐标.根据上述定义,请解答下列问题:
如图②,平面直角坐标系xoy内,直线l1的关系式为y=x,直线l2的关系式为
 ,M是平面直角坐标系内的点.
,M是平面直角坐标系内的点.(1)若p=q=0,求距离坐标为[0,0]时,点M的坐标;
(2)若q=0,且p+q=m(m>0),利用图②,在第一象限内,求距离坐标为[p,q]时,点M的坐标;
(3)若
 ,则坐标平面内距离坐标为[p,q]时,点M可以有几个位置?并用三角尺在图③画出符合条件的点M(简要说明画法).
,则坐标平面内距离坐标为[p,q]时,点M可以有几个位置?并用三角尺在图③画出符合条件的点M(简要说明画法).
【答案】分析:(1)根据题意可得此时M在两直线的交点位置.
(2)由题意可得此时点M在直线l2上,根据l2的解析式设出M点坐标,再根据k的几何意义可得出M点坐标.
(3)运用平行线的知识进行此问的解答.
解答:解:(1)∵p=q=0
∴点M是l1和l2的交点,故M(0,0)
(2)∵q=0
∴点M在l2上,
如图②,在第一象限内取点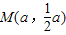 ,过点M作MA⊥l1交l1于点A,过点M作BC∥y轴
,过点M作MA⊥l1交l1于点A,过点M作BC∥y轴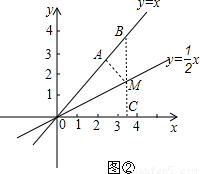 交l1、x轴于点B、C
交l1、x轴于点B、C
则OC=BC
∵q=0,p+q=m(m>0)
∴p=0,
即MA=m,
∵∠B=45°,
∴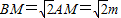 ,
,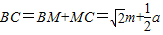
由OC=BC得a=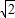 m+
m+ a,解得a=2
a,解得a=2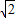 m,
m,
则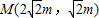
(3)点M有4个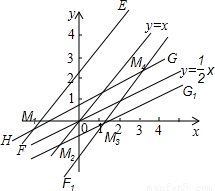
画法:
①分别过点 、
、 作与直线l1平行的直线EF、E1F1(与l1距离为1)
作与直线l1平行的直线EF、E1F1(与l1距离为1)
②分别过点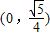 、
、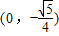 作与直线l2平行的直线GH、G1H1(与l2距离为
作与直线l2平行的直线GH、G1H1(与l2距离为 )
)
③直线EF、E1F1、GH、G1H1的4个交点M1、M2、M3、M4就是符合条件的点.
点评:本题考查了一次函数的知识,综合性较强,难度较大,同学们要注意细心地进行题干的分析,然后根据题意解答.
(2)由题意可得此时点M在直线l2上,根据l2的解析式设出M点坐标,再根据k的几何意义可得出M点坐标.
(3)运用平行线的知识进行此问的解答.
解答:解:(1)∵p=q=0
∴点M是l1和l2的交点,故M(0,0)
(2)∵q=0
∴点M在l2上,
如图②,在第一象限内取点
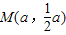 ,过点M作MA⊥l1交l1于点A,过点M作BC∥y轴
,过点M作MA⊥l1交l1于点A,过点M作BC∥y轴 交l1、x轴于点B、C
交l1、x轴于点B、C则OC=BC
∵q=0,p+q=m(m>0)
∴p=0,
即MA=m,
∵∠B=45°,
∴
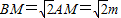 ,
,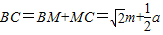
由OC=BC得a=
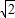 m+
m+ a,解得a=2
a,解得a=2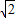 m,
m,则
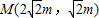
(3)点M有4个

画法:
①分别过点
 、
、 作与直线l1平行的直线EF、E1F1(与l1距离为1)
作与直线l1平行的直线EF、E1F1(与l1距离为1)②分别过点
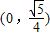 、
、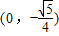 作与直线l2平行的直线GH、G1H1(与l2距离为
作与直线l2平行的直线GH、G1H1(与l2距离为 )
)③直线EF、E1F1、GH、G1H1的4个交点M1、M2、M3、M4就是符合条件的点.
点评:本题考查了一次函数的知识,综合性较强,难度较大,同学们要注意细心地进行题干的分析,然后根据题意解答.

练习册系列答案
相关题目