题目内容
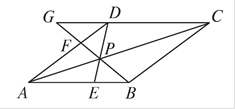
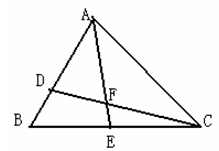
如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长BP交边AD于点F,交CD的延长线于点G.
(1)求证:△APB≌△APD;
(2)已知DF∶FA=1∶2,设线段DP的长为x,线段PF的长为y.
①求y与x的函数关系式;
②当x=6时,求线段FG的长.
(1)求证:△APB≌△APD;
(2)已知DF∶FA=1∶2,设线段DP的长为x,线段PF的长为y.
①求y与x的函数关系式;
②当x=6时,求线段FG的长.

(1)证明见解析;(1)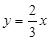 ;5.
;5.
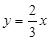 ;5.
;5.试题分析:(1)根据菱形的性质得出∠DAP=∠PAB,AD=AB,再利用全等三角形的判定得出△APB≌△APD;
(2)①首先证明△DFP≌△BEP,进而得出
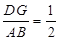 ,
,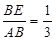 ,进而得出
,进而得出 ,即
,即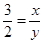 ,即可得出答案;
,即可得出答案;②根据①中所求得出PF=PE=4,DP=PB=6,进而得出
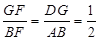 ,求出即可.
,求出即可.试题解析:(1)证明:∵点P是菱形ABCD对角线AC上的一点,
∴∠DAP=∠PAB,AD=AB,
∵在△APB和△APD中
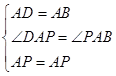 ,
,∴△APB≌△APD(SAS);
(2)解:①∵△APB≌△APD,
∴DP=PB,∠ADP=∠ABP,
∵在△DFP和△BEP中,
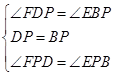 ,
,∴△DFP≌△BEP(ASA),
∴PF=PE,DF=BE,
∵四边形ABCD是菱形,
∴GD∥AB,
∴
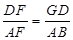 ,
,∵DF:FA=1:2,
∴
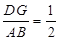 ,
,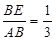 ,
,∴
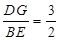 ,
,∴
 ,即
,即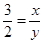 ,
,∴
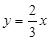 ;
;②当x=6时,
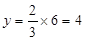 ,
,∴PF=PE=4,DP=PB=6,
∵
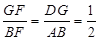 ,
,∴
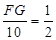 ,
,解得:FG=5,
故线段FG的长为5.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目

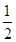 B、1 C、
B、1 C、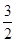 D、2
D、2 ,相似比为1:2,则
,相似比为1:2,则 与
与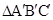 的面积的比为( )
的面积的比为( )