题目内容
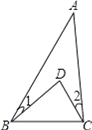
【题目】如图,在△ABC中,AB=AC,∠ABC=72°. 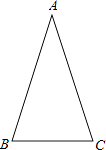
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.
【答案】
(1)解:①一点B为圆心,以任意长长为半径画弧,分别交AB,BC于点E,F;
②分别以点E,F为圆心,以大于 ![]() EF为半径画圆,两圆相交于点G,连接BG角AC于点D即可
EF为半径画圆,两圆相交于点G,连接BG角AC于点D即可
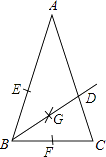
(2)解:∵在△ABC中,AB=AC,∠ABC=72°,
∴∠A=180°﹣2∠ABC=180°﹣144°=36°,
∵BD是∠ABC的平分线,
∴∠ABD= ![]() ∠ABC=
∠ABC= ![]() ×72°=36°,
×72°=36°,
∵∠BDC是△ABD的外角,
∴∠BDC=∠A+∠ABD=36°+36°=72°.
【解析】(1)根据角平分线的作法利用直尺和圆规作出∠ABC的平分线即可;(2)先根据等腰三角形的性质及三角形内角和定理求出∠A的度数,再由角平分线的定义得出∠ABD的度数,再根据三角形外角的性质得出∠BDC的度数即可.
【考点精析】通过灵活运用等腰三角形的性质,掌握等腰三角形的两个底角相等(简称:等边对等角)即可以解答此题.

练习册系列答案
相关题目