Question

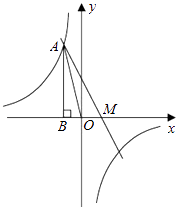
【题目】如图，在平面直角坐标系中，长方形MNPO的边OM在x轴上，边OP在y轴上，点N的坐标为（3，9），将矩形沿对角线PM翻折，N点落在F点的位置，且FM交y轴于点E，那么点F的坐标为_____．

Answer 1

【答案】（﹣，）

【解析】

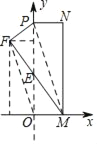
作FH⊥OP于H，FG⊥x轴于G．首先证明△PFE≌△MOE，推出OE＝FE，OM＝PF＝3，设OE＝x，那么PE＝9x，DE＝x，在Rt△PFE中，PE2＝FE2＋PF2，构建方程求出x即可解决问题.

如图，作FH⊥OP于H，FG⊥x轴于G，

∵点N的坐标为（3，9），

∴MO＝3，MN＝9，

根据折叠可知：PF＝OM，

而∠PFE＝∠MOE＝90°，∠FEP＝∠MEO，

∴△PFE≌△MOE，

∴OE＝FE，OM＝PF＝3，

设OE＝x，那么PE＝9x，DE＝x，

∴在Rt△PFE中，PE2＝FE2＋PF2，

∴（9x）2＝x2＋32，

∴x＝4，

∴EF＝4，PE＝5，

∴FH＝＝，

∴HE＝，

∴FG＝HO＝4＋＝，

∴F（，），

故答案为（，）．