题目内容
【题目】如图,已知等腰直角三角形△ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆☉O的直径.
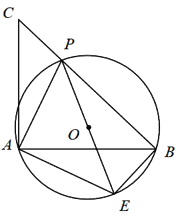
(1)求证:△APE是等腰直角三角形;
(2)证明△APC≌△AEB;
(3)若☉O的直径为2,求PC2+PB2的值
【答案】(1)见解答;(2)见解答; (3)4
【解析】
(1)由等腰直角三角形△ABC,得∠C=∠ABP=45°,则∠AEP=∠ABP=45°,由∠PAE=90°,即可解决问题;
(2)由(1)知,AP=AE,∠PAC=∠BAE,又AC=AB,即可得到△APC≌△AEB;
(3)由(2)得CP=BE,又PE是直径,则△PBE是直角三角形,则![]() ,即可得到
,即可得到![]() .
.
解:(1)在等腰直角三角形△ABC中,
∴∠C=∠ABP=45°,∠BAC=90°,
∴∠AEP=∠ABP=45°,
∵PE是直径,
∴∠PAE=90°,
∴∠APE=∠AEP=45°,
∴AP=AE,
∴△APE是等腰直角三角形.
(2)∵△ABC与△APE是等腰直角三角形
∴AP=AE,AC=AB,∠CAB=∠PAE=90°,
∴∠CAB-∠PAB=∠PAE-∠PAB,
即∠PAC=∠BAE,
∴△APC≌△AEB;
(3)由△APC≌△AEB,得CP=BE,
∴PE是直径,
∴∠PBE=90°,则△PBE是直角三角形,
∴![]() ,
,
∵CP=BE,PE=2,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目