题目内容
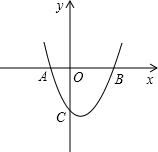
（1）用配方法把二次函数y=x2-4x+3化为顶点式，并在直角坐标系中画出它的大致图象（要求所画图象的顶点、与坐标轴的交点位置正确）．
（2）若A（x1，y1），B（x2，y2）是函数y=x2-4x+3图象上的两点，且x1＜x2＜1，请比较y1，y2的大小关系．（直接写结果）
（3）把方程x2-4x+3=2的根在函数y=x2-4x+3的图象上表示出来．
（2）若A（x1，y1），B（x2，y2）是函数y=x2-4x+3图象上的两点，且x1＜x2＜1，请比较y1，y2的大小关系．（直接写结果）
（3）把方程x2-4x+3=2的根在函数y=x2-4x+3的图象上表示出来．
（1）加上一次项系数一半的平方得，y=x2-4x+4-4+3，
配方得，y=（x-2）2-1（2分），
对称轴x=2，顶点（2，-1），
方程（x-2）2-1=0的解为x=3或1，
与x轴交点（1，0）、（3，0）与y轴交点（0，3）；
（2）如图，y1＞y2（2分）；
（3）∵方程x2-4x+3=2的根是当y=2时所对应的x的值，
∴画出直线y=2，与抛物线交点的横坐标即为方程的根．如图（2分）
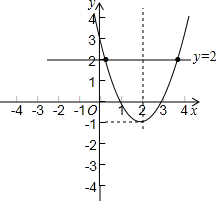
配方得，y=（x-2）2-1（2分），
对称轴x=2，顶点（2，-1），
方程（x-2）2-1=0的解为x=3或1，
与x轴交点（1，0）、（3，0）与y轴交点（0，3）；
（2）如图，y1＞y2（2分）；
（3）∵方程x2-4x+3=2的根是当y=2时所对应的x的值，
∴画出直线y=2，与抛物线交点的横坐标即为方程的根．如图（2分）
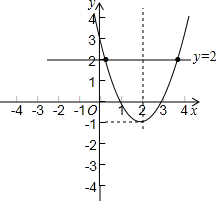
练习册系列答案
一线名师提优试卷系列答案
相关题目
