题目内容
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,AD+EC=AB.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;
(3)△DEF可能是等腰直角三角形吗?为什么?
(4)请你猜想:当∠A为多少度时,∠EDF+∠EFD=120°,并请说明理由.

【答案】(1)证明见解析;(2)∠DEF=70°; (3)△DEF不可能是等腰直角三角形,理由见解析;(4)当∠A=60°时,∠EDF+∠EFD=120°,理由见解析.
【解析】
(1)首先根据条件证明△DBE≌△ECF,根据全等三角形的性质可得DE=FE,进而可得到△DEF是等腰三角形;
(2)由(1)中的全等得出∠BDE=∠CEF,再由角之间的转化,从而可求解∠DEF的大小;(3)由于AB=AC,可得∠B=∠C≠90°=∠DEF,从而可确定其不可能是等腰直角三角形;
(4)先猜想出∠A的度数,则可得∠EDF+∠EFD=120°,根据前面的推导过程知∠EDF+∠EFD=120°时,∠DEF=60°,再由∠B=∠DEF以及等腰三角形的性质继而推得猜想的正确性.
(1)∵AB=AC,
∴∠B=∠C,
∵AD+EC=AB,AB=AD+BD,
∴BD=CE,
在△BDE和△CEF中,
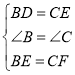 ,
,
∴△BDE≌△CEF(SAS)
∴DE=EF,
∴△DEF是等腰三角形;
(2)∵∠DEC=∠B+∠BDE,
即∠DEF+∠CEF=∠B+∠BDE,
由(1)知△BDE≌△CEF,
则∠BDE=∠CEF,
∴∠DEF=∠B,
∵∠A=40°,
∴∠B=∠C=![]() =70°,
=70°,
∴∠DEF=70°;
(3)△DEF不可能是等腰直角三角形,
∵AB=AC,
∴∠B=∠C≠90°,
由(2)知∠DEF=∠B,
∴∠DEF=∠B≠90°,
∴△DEF不可能是等腰直角三角形;
(4)当∠A=60°时,∠EDF+∠EFD=120°,
理由是:当∠EDF+∠EFD=120°时,
则∠DEF=180°-120°=60°,
∴∠B=∠DEF=60°,
∴∠A=180°-∠B-∠C=180°-60°-60°=60°,
∴当∠A=60°时,∠EDF+∠EFD=120°.

 阅读快车系列答案
阅读快车系列答案【题目】某校组织七年级学生体育健康抽测,(1)班25名学生的成绩(满分为100分)统计如下:
90,74,88,65,98,76,81,42,85,70,55,80,95,88,72,87,61,56,76,66,78,72,82,63,100.
(1)90分及以上为A级,75-89分为B级,60-74分为C级,60分以下为D级,请把下面表格补充完整,并将图中的条形图补充完整;
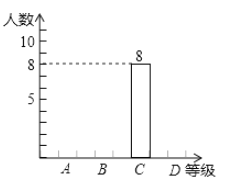
等级 | A | B | C | D |
人数 | 8 |
(2)该校七年级共有1000名学生,如果60分以上为合格,请估计七年级有多少人合格?
(3)请选择合适的统计图表示出抽测中每一个等级的人数占总人数的百分比.
【题目】“阶梯水价”充分发挥市场、价格因素在水资源配置、水需求调节等方面的作用,拓展了水价上调的空间,增强了企业和居民的节水意识,避免了水资源的浪费.阶梯式计量水价将水价分为两段或者多段,每一分段都有一个保持不变的单位水价,但是单位水价会随着耗水量分段而增加.某地“阶梯水价”收费标准如下表(按月计算):
用水量 (单位:m3 ) | 单价(元/m3 ) |
不超出 | 2 |
超出 | 3 |
超出 | 5 |
例如:该地区某户居民3月份用水![]() m3,则应交水费为
m3,则应交水费为![]() (元
(元![]() .
.
根据上表的内容解答下列问题:
(1)用户甲5月份用水16 m3,则该用户5月份应交水费多少元?
(2)用户乙5月份交水费50元,则该用户5月份的用水量为多少m3?
(3) 用户丙5、6两个月共用水![]() m3,其中6月份用水量超过了
m3,其中6月份用水量超过了![]() m3,设5月份用水
m3,设5月份用水![]() m3,请用含
m3,请用含![]() 的式子表示该户居民5、6两个月共交的水费.
的式子表示该户居民5、6两个月共交的水费.




