题目内容
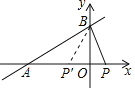
【题目】如图，直线y＝
x+3与坐标轴交于A，B两点，在射线AO上有一点P，当△APB是以AP为腰的等腰三角形时，点P的坐标是_____．
【答案】（﹣
，0）或（3
﹣6，0）．
【解析】
根据一次函数解析式求出A、B的坐标，再根据等腰三角形的腰分类讨论即可.
解：当y＝0时，x＝﹣6，即A（﹣6，0），
当x＝0时，y＝3，即B（0，3），
∴OA＝6，OB＝3，
在Rt△ABO中，AB＝
＝3，
若AP＝AB＝3，则OP＝AP﹣AO＝3﹣6，
∴点P（3﹣6，0）
若AP'＝BP'，在Rt△BP'O中，BP'2＝BO2+P'O2＝9+（AO﹣BP'）2．
∴BP'＝AP'＝
∴OP'＝，
∴P'（﹣，0）
综上所述：点P（﹣，0）或（3﹣6，0）
故答案为：（﹣，0）或（3﹣6，0）．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
