题目内容
 如图,A是反比例函数y=
如图,A是反比例函数y= (x>0)图象上一点,点B、D在 y轴正半轴上,△ABD是△COD关于点D的位似图形,且△ABD与△COD的位似比是1:3,△ABD的面积为1,则该反比例函数的表达式为________.
(x>0)图象上一点,点B、D在 y轴正半轴上,△ABD是△COD关于点D的位似图形,且△ABD与△COD的位似比是1:3,△ABD的面积为1,则该反比例函数的表达式为________.

分析:根据△ABD是△COD关于点D的位似图形,且△ABD与△COD的位似比是1:3,得出
 ,进而得出假设BD=x,AE=4x,D0=3x,AB=y,根据△ABD的面积为1,求出xy=2即可得出答案.
,进而得出假设BD=x,AE=4x,D0=3x,AB=y,根据△ABD的面积为1,求出xy=2即可得出答案.解答:
 解:过A作AE⊥x轴,
解:过A作AE⊥x轴,∵△ABD是△COD关于点D的位似图形,
且△ABD与△COD的位似是1:3,
∴
 ,
,∴OE=AB,
∴
 ,
,假设BD=x,AB=y
∴DO=3x,AE=4x,C0=3y,
∵△ABD的面积为1,
∴
 xy=1,
xy=1,∴xy=2,
∴AB•AE=4xy=8,
该反比例函数的表达式为:y=
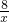 ,
,故答案为:y=
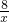 .
.点评:此题主要考查了位似图形的性质以及反比例函数的综合应用,得出假设BD=x,AE=4x,D0=3x,AB=y,根据△ABD的面积为1,求出xy=2是解决问题的关键.

练习册系列答案
相关题目
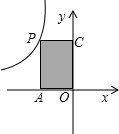 如图:P是反比例函数
如图:P是反比例函数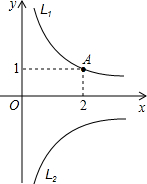 如图,L1是反比例函数y=
如图,L1是反比例函数y=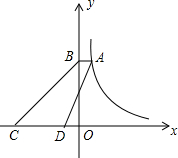 (2012•工业园区一模)如图,A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点C、D为x轴上动点,若CD=3AB,四边形ABCD的面积为4,则这个反比例函数的解析式为
(2012•工业园区一模)如图,A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点C、D为x轴上动点,若CD=3AB,四边形ABCD的面积为4,则这个反比例函数的解析式为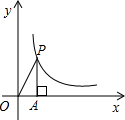 如图,P是反比例函数
如图,P是反比例函数 如图,A是反比例函数图象在第一象限内分支上的一点,过点A作y轴的垂线,垂足为B,点P在x轴上,若△ABP的面积为2,则这个反比例函数的解析式为
如图,A是反比例函数图象在第一象限内分支上的一点,过点A作y轴的垂线,垂足为B,点P在x轴上,若△ABP的面积为2,则这个反比例函数的解析式为