Question

【题目】如图，已知抛物线y＝ax2＋bx＋3的图象与x轴交于A、B两点，与y轴交于点C，且点C、D是抛物线上的一对对称点

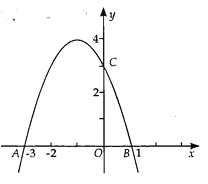
【1】求抛物线的解析式

【2】求点D的坐标，并在图中画出直线BD

【3】求出直线BD的一次函数解析式，并根据图象回答：当x满足什么条件时，上述二次函数的值大于该一次函数的值

Answer 1

【答案】

【1】

【2】 D(－2，3) 画出直线BD如图

【3】 BD的解析式为当－2<x<1时，二次函数的值大于该一次函数的值

【解析】

（1）将A、B的坐标代入抛物线的解析式中即可求得待定系数的值，

（2）进而可根据抛物线的对称轴求出D点的坐标；

（3）设出直线BD的一次函数解析式为y=kx+b，把B（1，0），D（-2，3）分别代入得可求出k，b，问题的解．由图象可知二次函数的值大于该一次函数的值时：-2＜x＜1。

解答：

（1）二次函数y=ax2+bx+3的图象经过点A（-3，0），B（1，0）

∴9a-3b+3="0" ，a+b+3=0；解得a=-1 、b=-2；

∴二次函数图象的解析式为y=-x2-2x+3；

（2）∵y=-x2-2x+3，

∴图象与y轴的交点坐标为（0，3）

∵点C、D是抛物线上的一对对称点．对称轴x=-b/2a=-1，

∴D点的坐标为（-2，3）．

（3）设直线BD的一次函数解析式为y=kx+b

把B（1，0），D（-2，3）分别代入得：0=k+b、3=-2k+b

解得：k=-1，b=1。

∴BD的解析式为y=-x+1。

由图象可知二次函数的值大于该一次函数的值时：-2＜x＜1。