��Ŀ����
����Ŀ��ѧУ��ͼ�����ͬһ����ֱ��·�ϣ��״�ѧУȥͼ��ݣ��Ҵ�ͼ��ݻ�ѧУ���ס������˶����ٲ�����ͬʱ���������ȵ���Ŀ�ĵأ�����֮��ľ���y���ף���ʱ��t�����ӣ�֮��ĺ�����ϵ��ͼ��ʾ��
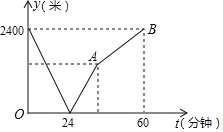
��1������ͼ����Ϣ����t���� ������ʱ�����������������ٶ�Ϊ�� ����/���ӣ��ҵ��ٶ�Ϊ�� ����/���ӣ�
��2��ͼ�е�A������Ϊ�� ����
��3�����߶�AB��ֱ�ߵĺ�������ʽ��
��4�������������У���ʱ�������400�ף�
���𰸡���1��24��40��60����2����40��1600������3���߶�AB����ʾ�ĺ�������ʽΪy��40x����4�������������У���20���Ӻ�28����ʱ�������400��
��������
��1������ͼ����Ϣ����![]() ����ʱ����������������60������ʻ2400�ף������ٶ�
����ʱ����������������60������ʻ2400�ף������ٶ�![]() ·��
·��![]() ʱ��ɵü��ٶȣ���������ҵ��ٶȣ�
ʱ��ɵü��ٶȣ���������ҵ��ٶȣ�
��2������Ҵ�ͼ��ݻ�ѧУ��ʱ�伴![]() ��ĺ����ꣻ
��ĺ����ꣻ
��3�����ô���ϵ������⼴�ɣ�
��4��������ǰ�����������ɣ�
�⣺��1������ͼ����Ϣ����t��24����ʱ�����������������ٶ�Ϊ2400��60��40����/���ӣ���
���ס������˵��ٶȺ�Ϊ2400��24��100��/���ӣ�
���ҵ��ٶ�Ϊ100��40��60����/���ӣ���
�ʴ�Ϊ��24��40��60��
��2���Ҵ�ͼ��ݻ�ѧУ��ʱ��Ϊ2400��60��40�����ӣ���
40��40��1600��
��A���������40��1600����
�ʴ�Ϊ����40��1600����
��3�����߶�AB����ʾ�ĺ�������ʽΪy��kx+b��
��A��40��1600����B��60��2400����
��![]() �����
�����![]() ��
��
���߶�AB����ʾ�ĺ�������ʽΪy��40x��
��4�������������ӭ�棺��2400��400����100��20�����ӣ���
���߹�����2400+400����100��28�����ӣ���
�������������У���20���Ӻ�28����ʱ�������400�ף�

����Ŀ��ˮ������Ϊ��ѡ����Ӧ�г������С���������磬������������ͬ������£�������Ʒ�ֵ�С�����������300��ֱ���ֲ�ڼס���������������г���Ϊ��ע�IJ����Ͳ������ȶ��ԣ������˳������飬�������£��벹��������
�ռ����� �Ӽס�������������ռ���25�������ϵ�С�������ĸ�����
�� 26 32 40 51 44 74 44 63 73 74 81 54 62 41 33 54 43 34 51 63 64 73 64 54 33
�� 27 35 46 55 48 36 47 68 82 48 57 66 75 27 36 57 57 66 58 61 71 38 47 46 71
�������������� �����·���������������������������
���� ���� ���� |
|
|
|
|
|
|
�� | 5 | 5 | 5 | 5 | 4 | 1 |
�� | 2 | 4 | 6 | 2 |
��˵����45������Ϊ�������ϸ�45��������Ϊ�����ϸ�����45��65��Ϊ�������ã�65��85��Ϊ�������㣩
�������� �����������ݵ�ƽ�����������ͷ������±���ʾ��
���� | ƽ���� | ���� | ���� |
�� | 53 | 54 | 3047 |
�� | 53 | 57 | 3022 |
�ó����ۣ���1�������Ҵ�����������������Ϊ__________�ꣻ
��2�������ƶϳ�__________�����С����������Ʒ�ָ���Ӧ�г���������Ϊ_____________________�������ٴ�������ͬ�ĽǶ�˵���ƶϵĺ����ԣ�