题目内容
【题目】抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P为抛物线上,且位于x轴下方.
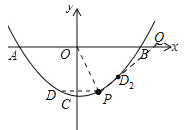
(1)如图1,若P(1,-3)、B(4,0),
① 求该抛物线的解析式;
② 若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
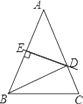
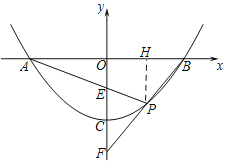
(2) 如图2,已知直线PA、PB与y轴分别交于E、F两点.当点P运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.

【答案】(1)①y=![]() x2-
x2-![]() ;②点D的坐标为(-1,-3)或(
;②点D的坐标为(-1,-3)或(![]() ,
,![]() );(2)是定值,等于2.
);(2)是定值,等于2.
【解析】
试题分析:(1)①将P(1,-3)、B(4,0)代入y=ax2+c得方程组,解方程组即可求得a、c的值,就求得函数解析式;②分两种情况求得点D的坐标即可;(2)设B(b,0),则A(-b,0)有ab2+c=0,即可得b2=![]() ,过点P(x0,y0)作PH⊥AB,有
,过点P(x0,y0)作PH⊥AB,有![]() ,利用相似三角形的性质分别求得OE、OF的值,即可得
,利用相似三角形的性质分别求得OE、OF的值,即可得![]() 的值.
的值.
试题解析:(1)①将P(1,-3)、B(4,0)代入y=ax2+c得
![]() ,解得
,解得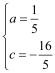 ,抛物线的解析式为:
,抛物线的解析式为:![]() .
.
②如图:
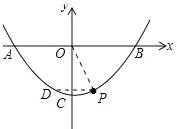
由∠DPO=∠POB得DP∥OB,D与P关于y轴对称,P(1,-3)得D(-1,-3);
如图,D在P右侧,即图中D2,则∠D2PO=∠POB,延长PD2交x轴于Q,则QO=QP,
设Q(q,0),则(q-1)2+32=q2,解得:q=5,∴Q(5,0),则直线PD2为![]() ,再联立
,再联立 得:x=1或
得:x=1或![]() ,∴ D2(
,∴ D2(![]() )
)
∴点D的坐标为(-1,-3)或(![]() )
)
(2)设B(b,0),则A(-b,0)有ab2+c=0,∴b2=![]() ,过点P(x0,y0)作PH⊥AB,有
,过点P(x0,y0)作PH⊥AB,有![]() ,易证:△PAH∽△EAO,则
,易证:△PAH∽△EAO,则 ![]() 即
即![]() ,∴
,∴![]() ,
,
同理得![]() ∴
∴![]() ,∴
,∴![]() ,则OE+OF=
,则OE+OF=![]()
∴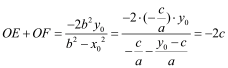 ,又OC=-c,∴
,又OC=-c,∴![]() .
.
∴![]() 是定值,等于2.
是定值,等于2.

练习册系列答案
相关题目