Question

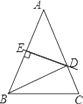
【题目】如图，△ABC中，AB=AC，AB的垂直平分线DE分别交AC、AB于点D、E．

（1）若∠A=46°，求∠CBD的度数；

（2）若AB=8，△CBD周长为13，求BC的长．

Answer 1

【答案】(1) 21°；(2)5

【解析】试题分析：（1）根据三角形内角和定理求出∠ABC=∠C=65°，根据线段垂直平分线的性质得到DA=DB，求出∠ABD的度数，计算即可；
（2）根据线段垂直平分线的性质和三角形的周长公式计算即可．

试题解析：（1）∵AB=AC，∠A=46°，
∴∠ABC=∠C=67°，
又∵DE垂直平分AB，
∴DA=DB，
∴∠ABD=∠A=46°，
∴∠DBC=21°；
（2）∵DE垂直平分AB，
∴DA=DB，
∴DB+DC=DA+DC=AC，
又∵AB=AC=8，△CBD周长为13，
∴BC=5．