Question

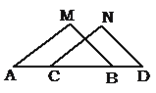
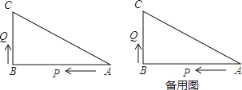
【题目】二次函数y=ax2+bx+c（a≠0）和正比例函数y= x的图象如图所示，则方程ax2+（b﹣ ）x+c=0（a≠0）的两根之和（ ）
A.大于0
B.等于0
C.小于0
D.不能确定

Answer 1

【答案】C
【解析】解：设ax2+bx+c=0（a≠0）的两根为x1 ， x2 ，
∵由二次函数的图象可知x1+x2＞0，a＞0，
∴﹣ ＞0．设方程ax2+（b﹣ ）x+c=0（a≠0）的两根为a，b，则a+b=﹣ =﹣ + ，
∵a＞0，
∴ ＞0，
∴a+b＞0．
故选C．
【考点精析】掌握抛物线与坐标轴的交点是解答本题的根本，需要知道一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．