题目内容
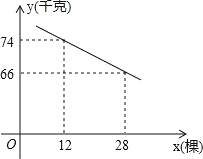
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示.
(1)求y与x之间的函数关系式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
【答案】(1) y=﹣0.5x+80;(2)增种果树10棵时,果园可以收获果实6750千克;(3)当增种果树40棵时果园的最大产量是7200千克.
【解析】
试题分析:(1)函数的表达式为y=kx+b,把点(12,74),(28,66)代入解方程组即可.(2)列出方程解方程组,再根据实际意义确定x的值.(3)构建二次函数,利用二次函数性质解决问题.
试题解析:(1)设函数的表达式为y=kx+b,该一次函数过点(12,74),(28,66),
得![]() ,
,
解得![]() ,
,
∴该函数的表达式为y=﹣0.5x+80,
(2)根据题意,得,
(﹣0.5x+80)(80+x)=6750,
解得,x1=10,x2=70
∵投入成本最低.
∴x2=70不满足题意,舍去.
∴增种果树10棵时,果园可以收获果实6750千克.
(3)根据题意,得
w=(﹣0.5x+80)(80+x)
=﹣0.5 x2+40 x+6400
=﹣0.5(x﹣40)2+7200
∵a=﹣0.5<0,则抛物线开口向下,函数有最大值
∴当x=40时,w最大值为7200千克.
∴当增种果树40棵时果园的最大产量是7200千克.

练习册系列答案
相关题目