Question

【题目】如图所示，二次函数y=ax2+bx+c的图象开口向上，图象经过点（﹣1，2）和（1，0），且与y轴交于负半轴，给出六个结论：①a＞0；②b＞0；③c＞0；④a+b+c=0；⑤b2﹣4ac＞0；⑥2a﹣b＞0，其中正确结论序号是_____．

Answer 1

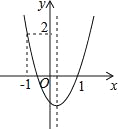
【答案】①④⑤⑥

【解析】

根据抛物线开口方向对①进行判断；由于二次函数的图象经过点和，且与轴交于负半轴，则抛物线的对称轴在轴的右侧，得到，可对②进行判断；根据抛物线与轴的交点在轴下方可对③进行判断；根据二次函数的图象经过可对④进行判断，根据与轴交点的个数对⑤进行判断，由①②的结果可判断⑥．

∵抛物线开口向上，∴，所以①正确；

∵二次函数的图象经过点和，∴抛物线的对称轴在轴的右侧，∴，∴，所以②错误；

∵抛物线与轴的交点在轴下方，∴，所以③错误；

∵抛物线经过，∴，所以④正确；

∵抛物线与轴有两个交点，∴，所以⑤正确；

∵，，∴，所以⑥正确．

综上所述：正确的①④⑤⑥．

故答案为：①④⑤⑥．